Giải SBT Toán 10 KNTT Bài 27. Thực hành tính xác suất theo định nghĩa cổ điển có đáp án
35 người thi tuần này 4.6 715 lượt thi 9 câu hỏi
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề kiểm tra Ôn tập chương 9 (có lời giải) - Đề 3
Đề kiểm tra Ôn tập chương 9 (có lời giải) - Đề 2
Đề kiểm tra Ôn tập chương 9 (có lời giải) -Đề 1
Đề kiểm tra Thực hành tính xác suất theo định nghĩa cổ điển (có lời giải) - Đề 3
Đề kiểm tra Thực hành tính xác suất theo định nghĩa cổ điển (có lời giải) - Đề 2
Đề kiểm tra Thực hành tính xác suất theo định nghĩa cổ điển (có lời giải) - Đề 1
Đề kiểm tra Biến cố và định nghĩa cổ điển của xác suất (có lời giải) -Đề 2
Đề kiểm tra Biến cố và định nghĩa cổ điển của xác suất (có lời giải) -Đề 2
Danh sách câu hỏi:
Lời giải
Theo đề bài ta có:
2x + y = 50 ⇔ y = 50 – 2x.
Sau một tiếng, trong quán có:
50 – (y – 6) + 2x – 5
= 50 – y + 6 + 2x – 5
= 51 + 2x – y (người)
Trong đó, có (2x – 5 + y) người là nữ. Vậy ta có xác suất để chọn được một khách nữ là:
⇔ 459 + 18x – 9y = 26x – 65 + 13y
⇔ 4x + 11y = 262
Mà y = 50 – 2x nên ta có:
4x + 11 . (50 – 2x) = 262
⇔ 18x = 288
⇔ x = 16
Do đó, y = 50 – 2 . 16 = 18.
Vậy x = 16, y = 18.
Lời giải
Số cách để chọn ngẫu nhiên hai em trong 40 em học sinh là: = 780 (cách).
Do đó, ta có n(Ω) = 780.
Gọi A là biến cố: “Hai em chọn được có một em nữ không thuận tay trái và một em nam thuận tay trái”
Lớp có 40 – 16 = 24 em nữ, trong đó, 24 – 2 = 22 em không thuận tay trái. Do đó, số cách chọn 1 em nữ không thuận tay trái là 22 cách.
Trong lớp có 3 em nam thuận tay trái, do đó, số cách chọn 1 em nam thuận tay trái là 3 cách.
Theo quy tắc nhân ta có: n(A) = 22 . 3 = 66.
Vậy xác suất của biến cố A là: P(A) = .
Lời giải
a)
Kí hiệu Đ, X, V tương ứng là viên bi màu đỏ, xanh, vàng.
Ta có sơ đồ hình cây mô tả các phần tử của không gian mẫu:
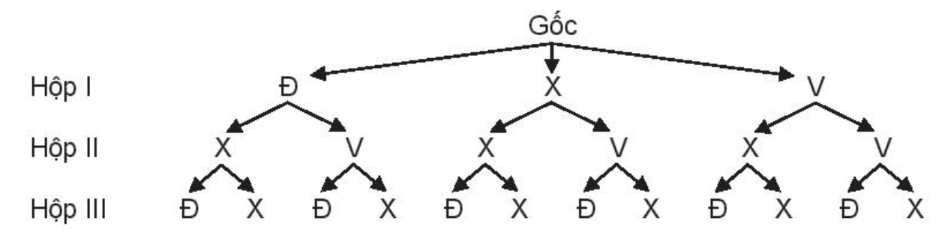
Do đó, ta có:
Ω = {(ĐXĐ; ĐXX; ĐVĐ; ĐVX; XXĐ; XXX; XVĐ; XVX; VXĐ; VXX; VVĐ; VVX}.
Vậy n(Ω) = 12.
Lời giải
b)
Gọi biến cố A: “Trong ba viên bi rút ra có ít nhất một viên bi đỏ”
Biến cố đối của A là : “Trong ba viên bi rút ra không có viên bi màu đỏ”.
Ta có: = {XXX; XVX; VXX; VVX}; n( ) = 4.
Do đó, ta có: P() =
Vậy P(A) =
Lời giải
Gọi a là số trên thẻ rút được từ hộp I, a ∈ {1; 2; 3}.
Gọi b là số trên thẻ rút được từ hộp II, b ∈ {2; 4; 6; 8}.
Gọi c là số trên thẻ rút được từ hộp III, c ∈ {1; 3; 5; 7; 9; 11}.
Ta có không gian mẫu: Ω = {(a, b, c) | a ∈ {1; 2; 3}, b ∈ {2; 4; 6; 8}, c ∈ {1; 3; 5; 7; 9; 11}}.
Theo quy tắc nhân, ta có: n(Ω) = 3 . 4 . 6 = 72.
Xét biến cố A: “Tổng ba số trên ba tấm thẻ là số lẻ”.
Do b luôn là một số chẵn và c luôn là một số lẻ nên tổng b + c luôn là một số lẻ, do đó để (a + b + c) là một số lẻ thì a phải là số chẵn. Do đó, a = 2.
Khi đó, A = {(2, b, c) | b ∈ {2; 4; 6; 8}, c ∈ {1; 3; 5; 7; 9; 11}}.
Do đó, n(A) = 1 . 4 . 6 = 24.
Vậy P(A) =
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.