Bài tập Bài 21. Đường tròn trong mặt phẳng tọa độ có đáp án
43 người thi tuần này 4.6 1.6 K lượt thi 14 câu hỏi
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
20 câu trắc nghiệm Toán 10 Cánh diều Bài tập cuối chương 7 (Đúng sai - trả lời ngắn) có đáp án
20 câu trắc nghiệm Toán 10 Cánh diều Bài 6. Ba đường conic (Đúng sai - trả lời ngắn) có đáp án
20 câu trắc nghiệm Toán 10 Cánh diều Bài 5. Phương trình đường trò (Đúng sai - trả lời ngắn) có đáp án
20 câu trắc nghiệm Toán 10 Cánh diều Bài 4. Vị trí tương đối và góc giữa hai đường thẳng. Khoảng cách từ một điểm đến một đường thẳng (Đúng sai - trả lời ngắn) có đáp án
20 câu trắc nghiệm Toán 10 Cánh diều Bài 3. Phương trình đường thẳn (Đúng sai - trả lời ngắn) có đáp án
20 câu trắc nghiệm Toán 10 Cánh diều Bài 2. Biểu thức tọa độ của các phép toán vectơ (Đúng sai - trả lời ngắn) có đáp án
20 câu trắc nghiệm Toán 10 Cánh diều Bài 1. Tọa độ của vectơ (Đúng sai - trả lời ngắn) có đáp án
20 câu trắc nghiệm Toán 10 Cánh diều Bài ôn tập cuối chương 6 (Đúng sai - trả lời ngắn) có đáp án
Danh sách câu hỏi:
Lời giải
Hướng dẫn giải
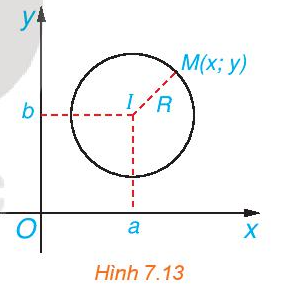
Điểm M thuộc đường tròn (C) khi khoảng cách từ tâm I của (C) đến M bằng bán kính R của (C).
Ta có: \(\overrightarrow {IM} = \left( {x - a;y - b} \right)\) nên \(IM = \sqrt {{{\left( {x - a} \right)}^2} + {{\left( {y - b} \right)}^2}} \).
Khi đó IM = R \( \Leftrightarrow \sqrt {{{\left( {x - a} \right)}^2} + {{\left( {y - b} \right)}^2}} = R\)\( \Leftrightarrow {\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} = {R^2}\) (do R > 0, (x – a)2 ≥ 0, (y – b)2 ≥ 0).
Vậy điểm M(x; y) thuộc đường tròn (C), tâm I(a; b), bán kính R khi và chỉ khi
(x – a)2 + (y – b)2 = R2.
Lời giải
Hướng dẫn giải
Ta viết phương trình (C) ở dạng (x – (– 2))2 + (y – 4)2 = \({\left( {\sqrt 7 } \right)^2}\).
Vậy (C) có tâm I(– 2; 4) và bán kính R = \(\sqrt 7 \).
Lời giải
Hướng dẫn giải
a) Phương trình x2 – y2 – 2x + 4y – 1 = 0 không có dạng x2 + y2 – 2ax – 2by + c = 0 nên đây không phải là phương trình đường tròn.
b) Ta có: x2 + y2 – 2x + 4y + 6 = 0
⇔ x2 + y2 – 2 . 1 . x – 2 . (– 2) . y + 6 = 0.
Có các hệ số a = 1, b = – 2, c = 6.
Ta có: a2 + b2 – c = 12 + (– 2)2 – 6 = – 1 < 0.
Vậy phương trình b) không phải là phương trình đường tròn.
c) x2 + y2 + 6x – 4y + 2 = 0
⇔ x2 + y2 – 2 . (– 3) . x – 2 . 2 y + 2 = 0.
Có các hệ số a = – 3, b = 2, c = 2.
Ta có: a2 + b2 – c = (– 3)2 + 22 – 2 = 11 > 0.
Do đó phương trình c) là phương trình đường tròn có tâm I(– 3; 2) và bán kính R = \(\sqrt {11} \).
Lời giải
Hướng dẫn giải
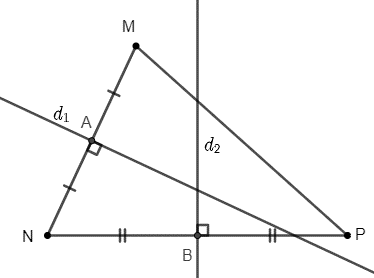
Các đoạn thẳng MN, NP tương ứng có trung điểm là A(3; – 3), B\(\left( {\frac{5}{2};\,\,\frac{{ - 9}}{2}} \right)\). Đường thẳng trung trực d1 của đoạn thẳng MN đi qua điểm A(3; – 3) và có vectơ pháp tuyến \(\overrightarrow {MN} = \left( { - 2;\,4} \right)\).
Vì \(\overrightarrow {MN} = \left( { - 2;4} \right)\) cùng phương với \(\overrightarrow {{n_1}} = \left( {1;\, - 2} \right)\) nên d1 cũng nhận \(\overrightarrow {{n_1}} = \left( {1;\, - 2} \right)\) là vectơ pháp tuyến. Do đó, phương trình của d1 là: 1(x – 3) – 2(y + 3) = 0 hay x – 2y – 9 = 0.
Đường thẳng trung trực d2 của đoạn thẳng NP đi qua B\(\left( {\frac{5}{2};\,\,\frac{{ - 9}}{2}} \right)\) và có vectơ pháp tuyến \(\overrightarrow {NP} = \left( {1;\, - 7} \right)\), do đó phương trình d2 là: \(1\left( {x - \frac{5}{2}} \right) - 7\left( {y + \frac{9}{2}} \right) = 0\) hay x – 7y – 34 = 0.
Tâm I của đường tròn (C) cách đều ba điểm M, N, P nên I là giao điểm của d1 và d2.
Vậy tọa độ của I là nghiệm của hệ phương trình \(\left\{ \begin{array}{l}x - 2y - 9 = 0\\x - 7y - 34 = 0\end{array} \right.\).
Suy ra I(– 1; – 5). Đường tròn (C) có bán kính là IM =\(\sqrt {{{\left( {4 - \left( { - 1} \right)} \right)}^2} + {{\left( { - 5 - \left( { - 5} \right)} \right)}^2}} = 5\).
Vậy phương trình của (C) là: (x + 1)2 + (y + 5)2 = 25.
Lời giải
Hướng dẫn giải
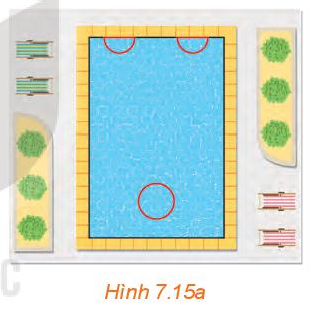
Gọi bán kính của bể hình tròn và bể nửa hình tròn tương ứng là x, y (m) (x, y > 0).
Chu vi của bể hình tròn là: 2πx = 2 . 3,14 . x = 6,28x (m).
Vì hai bể còn lại là hai bể có dạng nửa hình tròn bằng nhau nên tổng chu vi của hai bể này bằng tổng chu vi của đường tròn bán kính y (m) với 2 lần độ dài đường kính của đường tròn đó, do đó chu vi của hai bể nửa hình tròn là:
2πy + 2 . 2y = 2 . 3,14 . y + 4y = 10,28y (m).
Tổng chu vi của ba bể là 32 m nên ta có: 6,28x + 10,28y = 32 hay 1,57x + 2,57y – 8 = 0.
Diện tích của bể hình tròn là: πx2 = 3,14x2 (m2).
Diện tích của hai bể nửa hình tròn là: πy2 = 3,14y2 (m2).
Gọi tổng diện tích của ba bể sục là S (m2). Khi đó ta có:
3,14x2 + 3,14y2 = S hay x2 + y2 = \(\frac{S}{{3,14}}\).
Trong mặt phẳng tọa độ Oxy, xét đường tròn (C): x2 + y2 = \(\frac{S}{{3,14}}\) có tâm O(0; 0), bán kính R = \(\sqrt {\frac{S}{{3,14}}} \) và đường thẳng ∆: 1,57x + 2,57y – 8 = 0. Khi đó bài toán được chuyển thành: Tìm R nhỏ nhất để (C) và ∆ ít nhất một điểm chung, với hoành độ và tung độ đều là các số dương.
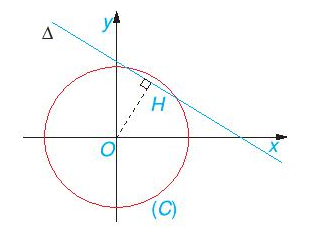
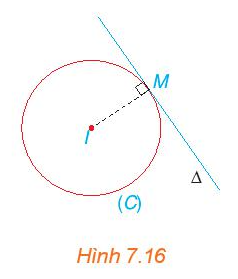
Bài toán trên tương đương với ∆ tiếp xúc với (C), đồng thời khi đó điểm M trùng với điểm H là hình chiếu vuông góc của O trên ∆.
Ta có: OH ⊥ ∆ nên .
Suy ra đường thẳng OH có một vectơ pháp tuyến là .
Phương trình đường thẳng OH là:
2,57(x – 0) – 1,57(y – 0) = 0 hay 2,57x – 1,57y = 0.
Điểm H là giao điểm của đường thẳng OH và đường thẳng ∆ nên tọa độ của H là nghiệm của hệ phương trình .
Giải hệ trên ta được .
Vậy bán kính bể sục hình tròn xấp xỉ bằng 1,38 m và bể sục nửa hình tròn xấp xỉ bằng 2,27 m thì thỏa mãn yêu cầu bài toán.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.