Bài tập Bài 19. Phương trình đường thẳng có đáp án
118 người thi tuần này 4.6 1.7 K lượt thi 16 câu hỏi
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề kiểm tra Ôn tập chương 9 (có lời giải) - Đề 3
Đề kiểm tra Ôn tập chương 9 (có lời giải) - Đề 2
Đề kiểm tra Ôn tập chương 9 (có lời giải) -Đề 1
Đề kiểm tra Thực hành tính xác suất theo định nghĩa cổ điển (có lời giải) - Đề 3
Đề kiểm tra Thực hành tính xác suất theo định nghĩa cổ điển (có lời giải) - Đề 2
Đề kiểm tra Thực hành tính xác suất theo định nghĩa cổ điển (có lời giải) - Đề 1
Đề kiểm tra Biến cố và định nghĩa cổ điển của xác suất (có lời giải) -Đề 2
Đề kiểm tra Biến cố và định nghĩa cổ điển của xác suất (có lời giải) -Đề 2
Danh sách câu hỏi:
Lời giải
Hướng dẫn giải
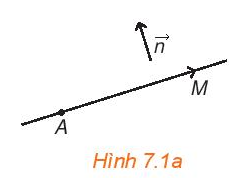
Ta có: \(\overrightarrow {AM} \bot \overrightarrow n \) nên đường thẳng AM vuông góc với giá của vectơ \(\overrightarrow n \).
Vậy tập hợp các điểm M thỏa mãn yêu cầu bài toán là đường thẳng đi qua điểm A và vuông góc với giá của vectơ \(\overrightarrow n \).
Lời giải
Hướng dẫn giải
Ta có: \(\overrightarrow {AM} = \left( {x - {x_0};y - {y_0}} \right)\).
Vì điểm M(x; y) thuộc ∆ ⇔ \(\overrightarrow n \bot \overrightarrow {AM} \)
\( \Leftrightarrow \overrightarrow n .\overrightarrow {AM} = 0\)
⇔ a.(x – x0) + b(y – y0) = 0.
Vậy điểm M(x; y) thuộc ∆ khi và chỉ khi a(x – x0) + b(y – y0) = 0.
Lời giải
Hướng dẫn giải
Ta có: \(\overrightarrow {BC} = \left( {6 - 2;1 - 3} \right) = \left( {4; - 2} \right)\).
Gọi đường cao kẻ từ đỉnh A của tam giác ABC là đường thẳng ∆, do đó ∆ ⊥ BC.
Suy ra đường thẳng ∆ đi qua điểm A(– 1; 5) và nhận vectơ \(\overrightarrow {BC} \) làm vectơ pháp tuyến.
Vậy phương trình tổng quát của đường thẳng ∆ là 4(x + 1) – 2(y – 5) = 0 hay 2x – y + 7 = 0.
Lời giải
Hướng dẫn giải
Ta có: y = 3x + 4 ⇔ 3x – y + 4 = 0.
Do đó đường thẳng ∆ có phương trình tổng quát: 3x – y + 4 = 0.
Vậy một vectơ pháp tuyến của ∆ là \(\overrightarrow n \left( {3; - 1} \right)\).
Lời giải
Hướng dẫn giải
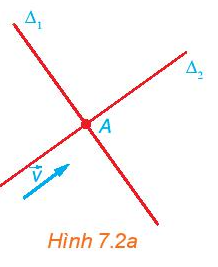
Quan sát Hình 7.2a ta thấy giá của vectơ song song với đường thẳng ∆2 nên vật thể chuyển động với vận tốc bằng \(\overrightarrow v \) và đi qua A thì nó di chuyển trên đường ∆2.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.