Giải SBT Toán 10 Bài 3. Bất phương trình bậc nhất hai ẩn có đáp án

Lời giải:

Biểu diễn miền nghiệm của bất phương trình $-$3x + y < 4 trên mặt phẳng tọa độ.

Bước 1. Vẽ đường thẳng d: $-$3x + y = 4 trên mặt phẳng tọa độ Oxy như sau:

• Xác định hai điểm thuộc đường thẳng d: $-$3x + y = 4.

Ta có bảng sau:

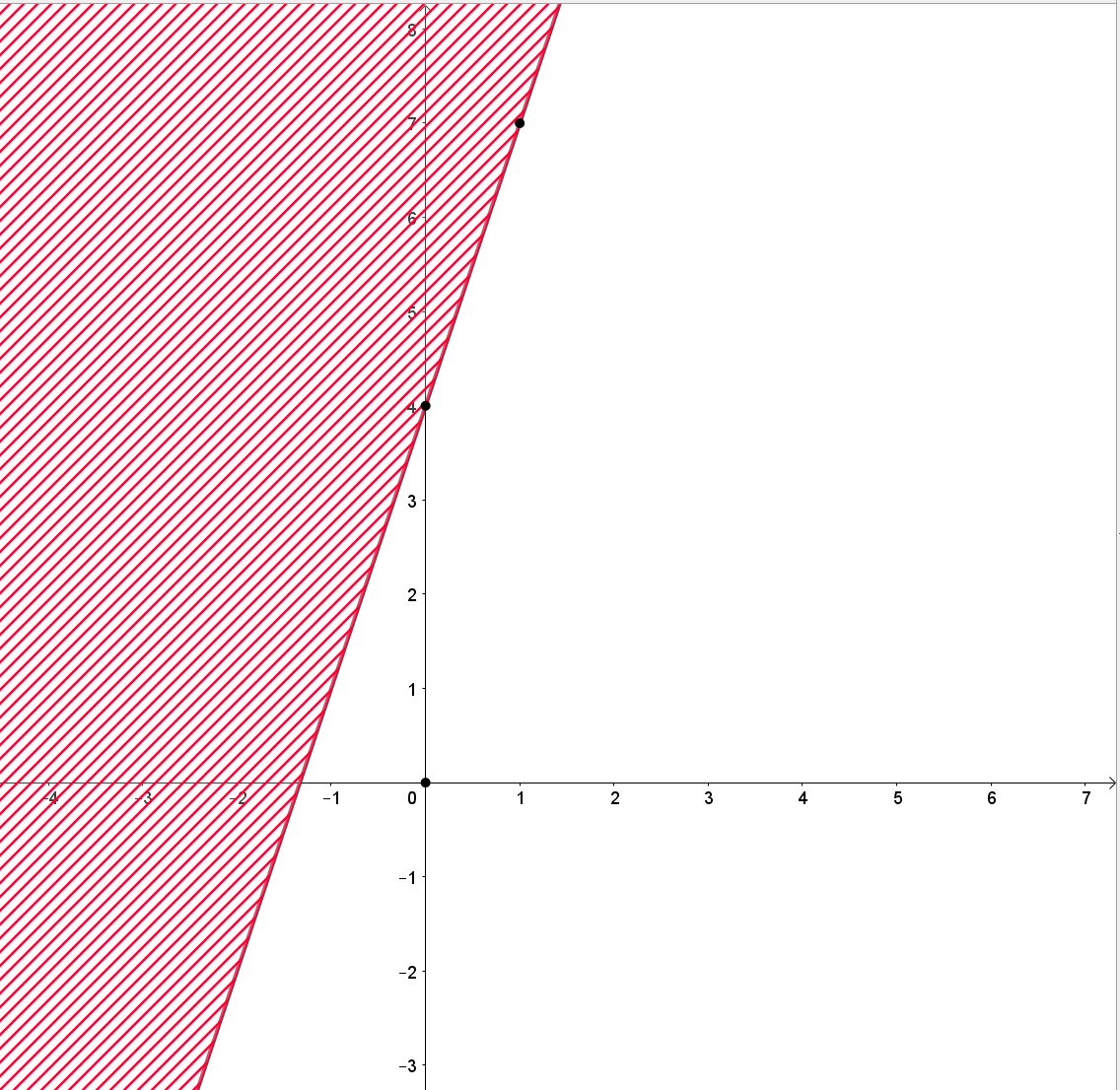
Do đó đồ thị của đường thẳng d: $-$3x + y = 4 đi qua các điểm có tọa độ (0; 4) và (1; 7).

• Xác định 2 điểm đó trên hệ trục tọa độ Oxy và kẻ đường thẳng đi qua 2 điểm đó, ta thu được đường thẳng d: -3x + y = 4.

Bước 2. Ta chọn O(0; 0) là điểm không thuộc đường thẳng d: -3x + y = 4 và thay vào biểu thức -3x + y, ta có -3 . 0 + 0 = 0 < 4.

Do đó miền nghiệm của bất phương trình -3x + y < 4 là nửa mặt phẳng bờ d chứa gốc tọa độ và bỏ đi đường thẳng d (miền không được gạch).

Lời giải:

Khi đó miền nghiệm của bất phương trình $-$3x + y ≤ 4 là nửa mặt phẳng bờ d chứa gốc tọa độ (miền không được gạch).

Miền nghiệm của bất phương trình $-$3x + y ≥ 4 là nửa mặt phẳng bờ d không chứa gốc tọa độ (miền được gạch).

Lời giải:

Ta có 2x + 3y + 3 ≤ 5x + 2y + 3

2x + 3y + 3$-$ 5x $-$2y $-$3 ≤ 0.

$-$3x + y ≤ 0.

Biểu diễn miền nghiệm của bất phương trình $-$3x + y ≤ 0 trên mặt phẳng tọa độ:

Bước 1. Vẽ đường thẳng d: $-$3x + y = 0 theo các bước sau:

• Xác định hai điểm thuộc đường thẳng d: $-$3x + y = 0.

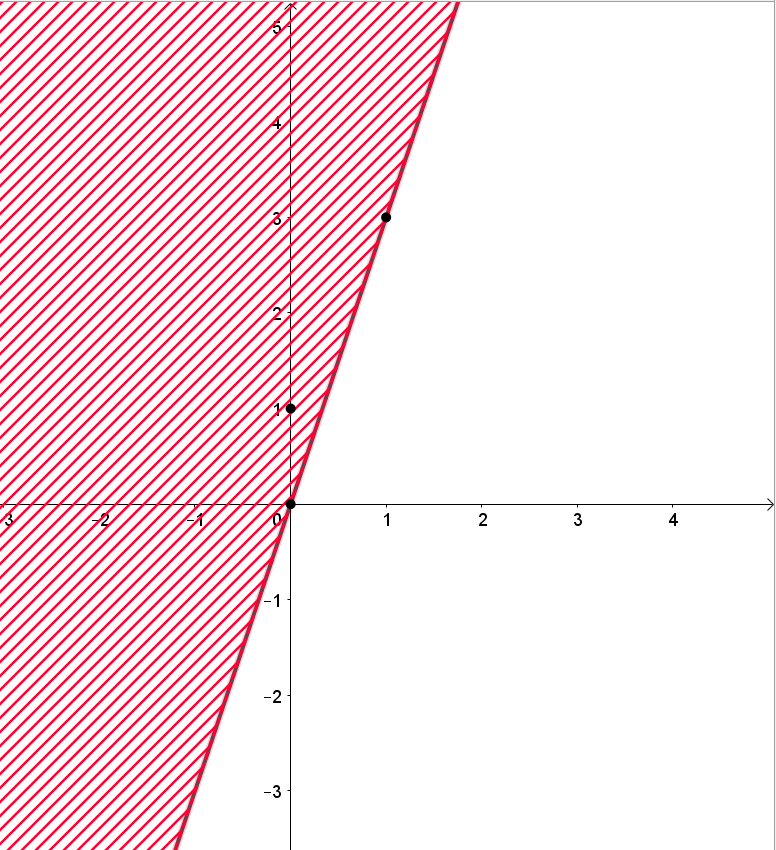
Do đó đường thẳng d: - 3x + y = 0 đi qua hai điểm có tọa độ (0; 0) và (1; 3).

• Xác định hai điểm đó trên hệ trục tọa độ Oxy, kẻ đường thẳng đi qua 2 điểm đó ta thu được đường thẳng d: - 3x + y = 0.

Bước 2. Ta chọn điểm (0; 1) là điểm không thuộc đường thẳng d: -3x + y = 0 và thay vào biểu thức -3x + y ta có -3 . 0 + 1 = 1 > 0.

Do đó miền nghiệm của bất phương trình -3x + y ≤ 0 là nửa mặt phẳng bờ d không chứa điểm (0; 1) (miền không được gạch).

Lời giải:

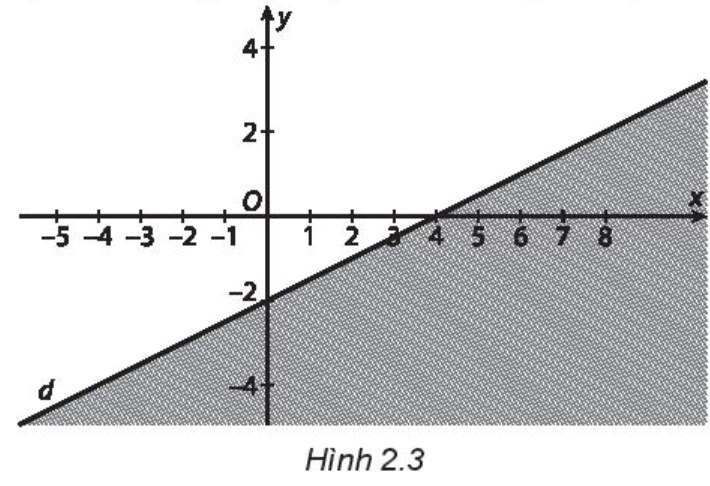
Ta thấy đường thẳng d đi qua hai điểm (0; -2) và (4; 0).

Gọi phương trình đường thẳng d: y = ax + b (a ≠ 0).

Thay x = 0; y = -2 vào đường thẳng d ta có:

-2 = a . 0 + b

b = -2.

Thay x = 4; y = 0 vào đường thẳng d ta có:

0 = 4 . a + (-2)

2 = 4 . a

a = \[\frac{2}{4} = \frac{1}{2}\]

Do đó phương trình đường thẳng d: y = \[\frac{1}{2}\]x - 2

2-y = x 4

x - 2y = 4.

Chọn điểm O(0; 0) là điểm không thuộc đường thẳng d và thay vào biểu thức x - 2y ta được: 0 - 2 . 0 = 0 < 4.

Do đó bất phương trình nhận nửa mặt phẳng bờ là đường thẳng d (miền không bị gạch) làm miền nghiệm là x - 2y ≤ 4.

Lời giải:

Biểu diễn miền nghiệm của bất phương trình x + 2y ≥ $-$4 trên mặt phẳng tọa độ:

Bước 1. Ta vẽ đường thẳng d: x + 2y = $-$4 theo các bước sau:

• Xác định hai điểm thuộc đường thẳng d.

Ta có bảng sau:

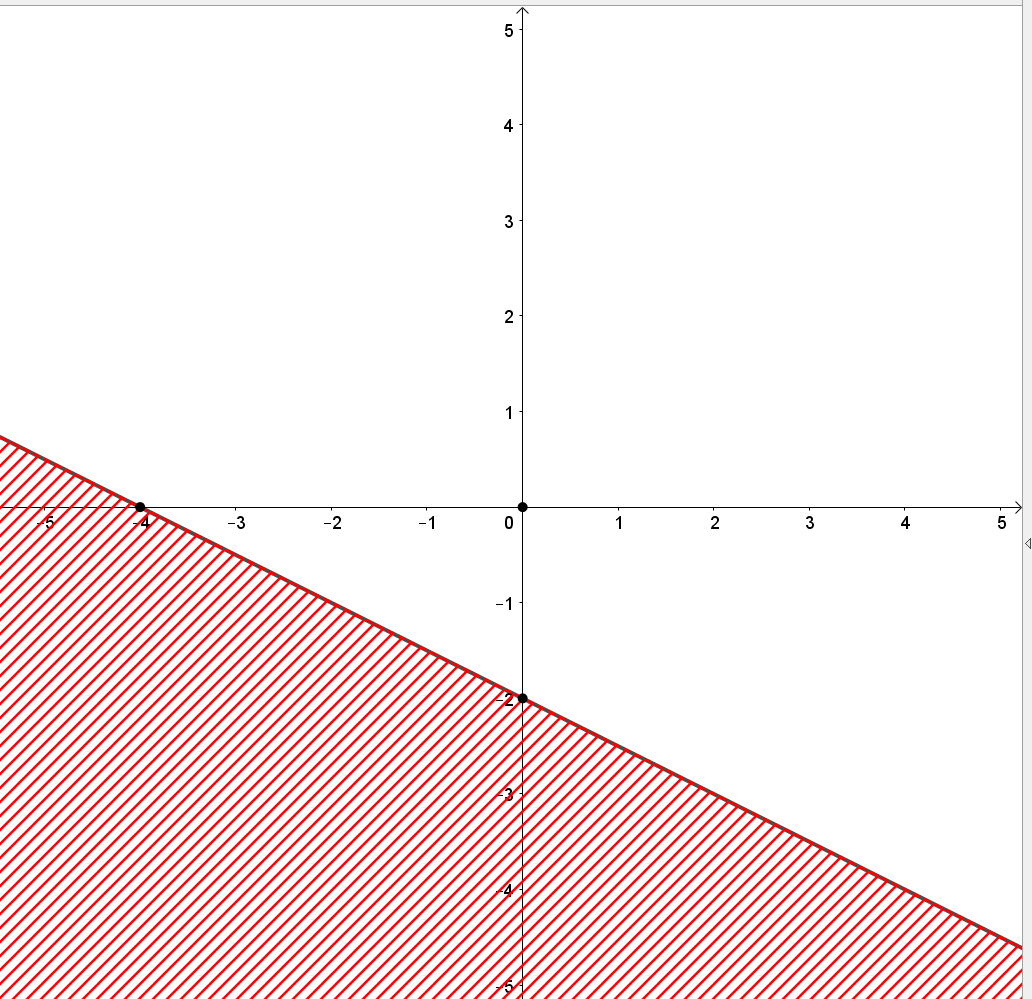
Do đó đường thẳng d: x + 2y = - 4 đi qua hai điểm (0; -2) và (-4; 0).

• Xác định hai điểm đó trên hệ trục tọa độ Oxy, kẻ đường thẳng đi qua 2 điểm đó ta thu được đường thẳng d: x + 2y = -4.

Bước 2. Chọn điểm O(0; 0) không thuộc đường thẳng d và thay vào biểu thức x + 2y ta được 0 + 2 . 0 = 0 > -4.

Do đó miền nghiệm của bất phương trình x + 2y ≥ -4 là nửa mặt phẳng bờ d chứa gốc tọa độ (miền không được gạch).

Lời giải:

Do x, y là các số nguyên âm và x + 2y ≥ $-$4 nên 0 > x > $-$4.

Với y ≤ $-$2 thì 2y ≤ $-$4, mà x là số nguyên âm nên x + 2y < $-$4 (loại).

Do đó 0 > y > $-$2 suy ra y = $-$1.

Ta có bảng sau:

Vậy miền nghiệm chứa hai điểm (x; y) {(-1; -1); (-2; -1)} với x, y là các số nguyên âm.