Bài tập Giá trị lượng giác của một góc từ 0 độ đến 180 độ có đáp án
48 người thi tuần này 4.6 2.3 K lượt thi 10 câu hỏi
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề kiểm tra Ôn tập chương 9 (có lời giải) - Đề 3
Đề kiểm tra Ôn tập chương 9 (có lời giải) - Đề 2
Đề kiểm tra Ôn tập chương 9 (có lời giải) -Đề 1
Đề kiểm tra Thực hành tính xác suất theo định nghĩa cổ điển (có lời giải) - Đề 3
Đề kiểm tra Thực hành tính xác suất theo định nghĩa cổ điển (có lời giải) - Đề 2
Đề kiểm tra Thực hành tính xác suất theo định nghĩa cổ điển (có lời giải) - Đề 1
Đề kiểm tra Biến cố và định nghĩa cổ điển của xác suất (có lời giải) -Đề 2
Đề kiểm tra Biến cố và định nghĩa cổ điển của xác suất (có lời giải) -Đề 2
Danh sách câu hỏi:
Lời giải
Sau bài học này ta sẽ trả lời được:
Với góc α cho trước, 0o < α < 180o.
Trên nửa đường tròn đơn vị, vẽ điểm M(x0; y0) sao cho .
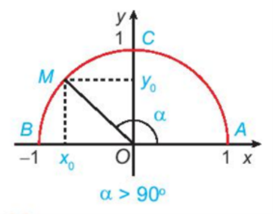
Khi đó: sinα = y0; cosα = x0;
tanα = (x0 ≠ 0); cotα = (y0 ≠ 0).
Lời giải
a)
Gọi điểm A có tọa độ A(1; 0).
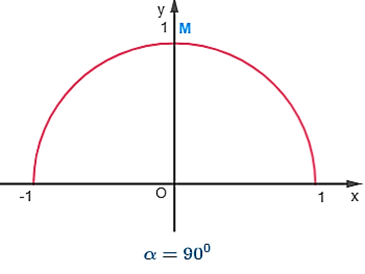
• α = 90o hay . Khi đó, điểm M có tọa độ M(0; 1).
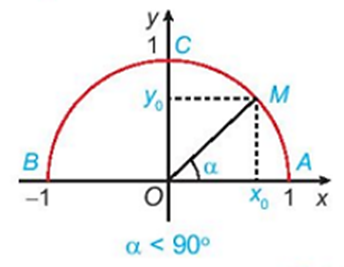
Do đó, điểm M(x0; y0) nằm trên cung tròn (không tính điểm C) thỏa mãn 0 < x0 ≤ 1, 0 ≤ y0 < 1.
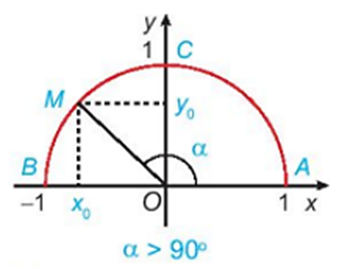
• α > 90o hay .
Do đó, điểm M(x0; y0) nằm trên cung tròn (không tính điểm C) thỏa mãn −1 ≤ x0 < 0, 0 ≤ y0 < 1.
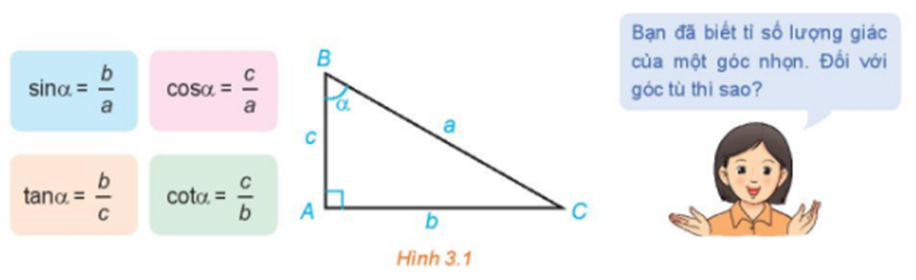
b) Khi 0o < α < 90o
Kẻ MH ^ Ox, MK ^ Oy (H Î Ox, H Î Oy). Khi đó .
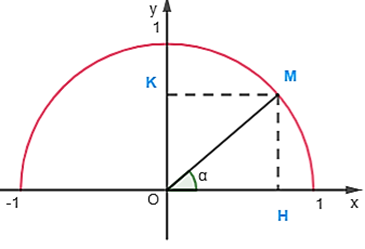
Gọi điểm M có tọa độ M(x0; y0).
Xét tứ giác MKOH có:
(Ox ^ Oy)
(MH ^ Ox)
(MK ^ Oy)
Do đó tứ giác MKOH là hình chữ nhật.
Suy ra OH = |x0| = x0; MH = OK = |y0| = y0.
Ta có OM = 1 (bán kính đường tròn đơn vị).
Xét ∆MHO vuông tại H, ta có:
.
Hay sin α = y0.
Ta lại có: .
Hay cos α = x0.
Vậy cos α là hoành độ của điểm M và sin α là tung độ của điểm M.
Lời giải
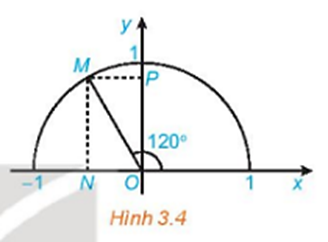
Gọi M là điểm trên nửa đường tròn đơn vị sao cho . Gọi H, K tương ứng là hình chiếu vuông của M lên các trục Ox, Oy.
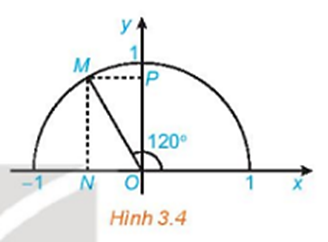 Điểm M nằm trên nửa đường tròn đơn vị sao cho .
Điểm M nằm trên nửa đường tròn đơn vị sao cho .
Hai điểm N, P tương ứng là hình chiếu vuông của M lên hai trục Ox, Oy.
Ta có: OM = 1 (bán kính đường tròn đơn vị).
Ta có .
Xét tam giác vuông MON, có:
+
+
.
Ta có điểm M nằm bên trái trục Oy (vì là góc tù).
Suy ra điểm M có tọa độ là M .
Suy ra
+
Lời giải
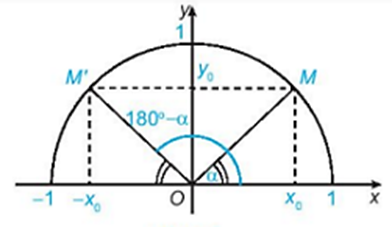
Hai điểm M và M’ đối xứng với nhau qua trục Oy.
Tọa độ của hai điểm M và M’ là: M(x0; y0), M’(–x0; y0).
Ta có: .
Khi đó:
∙ sin α = y0, cos α = x0.
∙ sin (180o – α) = y0, cos (180o – α) = –x0 hay x0 = – cos (180o – α).
Do đó: sin α = sin (180o – α) (= y0), cos α = – cos (180o – α) (= x0).
Vậy sin α = sin (180o – α), cos α = – cos (180o – α).
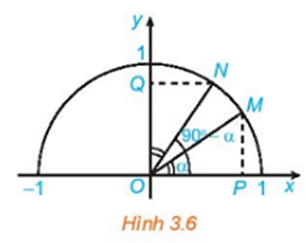
Lời giải
Ta có:
Dễ thấy: .
Xét ∆NOQ và ∆MOP có:
OM = ON = 1 (bán kính đường tròn đơn vị).
.
Do đó ΔNOQ = ΔMOP (cạnh huyền – góc nhọn)
Suy ra OP = OQ (hai cạnh tương ứng)
Ta có: OP = cos α, OQ = sin (90o – α).
Ta có: OP = , OQ =
.
Do đó: cos α = sin (90o − α).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.