Câu hỏi:

12/07/2024 59,929

Một chiếc đu quay có bán kính 75m, tâm của vòng quay ở độ cao 90m (H.3.7), thời gian thực hiện mỗi vòng quay của đu quay là 30 phút. Nếu một người vào Cabin tại vị trí thấp nhất của vòng quay, thì sau 20 phút quay người đó ở độ cao bao nhiêu mét?

Xem lời giải

Câu hỏi trong đề: Bài tập Giá trị lượng giác của một góc từ 0 độ đến 180 độ có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Giả sử chiếc đu quay quay theo chiều kim đồng hồ.

Gọi M là vị trí thấp nhất của cabin, M’ là vị trí của cabin sau 20 phút và các điểm A, A’, B, H (như hình vẽ).

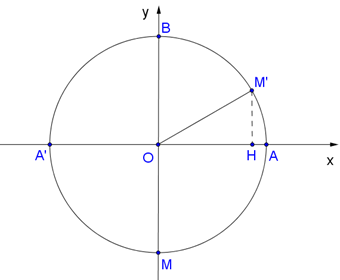
Một chiếc đu quay có bán kính 75m, tâm của vòng quay ở độ cao 90m (H.3.7) (ảnh 1)

Vì đi cả vòng quay mất 30 phút nên sau 20 phút, cabin sẽ đi quãng đường bằng chu vi đường tròn.

Sau 15 phút, cabin di chuyển từ điểm M đến điểm B, đi được chu vi đường tròn.

Trong 5 phút tiếp theo, cabin đi chuyển từ điểm B đến điểm M’ tương ứng chu vi đường tròn hay cung tròn .

Do đó: $\hat{B O M'} = \frac{1}{3} . 180^{o} = 60^{o}$

$\Rightarrow \hat{A O M'} = 90^{o} - 60^{o} = 30^{o}$

Ta có $M' H = \sin 30^{o} . O M' = \frac{1}{2} . 75 = 37,5$ (m).

Do đó, độ cao của người đó là:

37,5 + 90 = 127,5 (m).

Vậy sau 20 phút quay người đó ở độ cao 127,5 m.

Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

Bình luận

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Chứng minh các hệ thức sau:

a) $\sin^{2} α + \cos^{2} α = 1;$

b) $1 + \tan^{2} α = \frac{1}{{cos}^{2} α} (α \neq 90^{0});$

c) $1 + \cot^{2} α = \frac{1}{\sin^{2} α} (0^{0} < α < 180^{0}) .$

Xem đáp án

Lời giải

Chứng minh các hệ thức sau: a) sin^2 alpha + cos^2 alpha = 1; (ảnh 1)

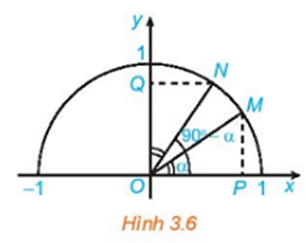
Lấy điểm M trên đường tròn lượng giác sao cho $\hat{x O M} = α$ . Từ M kẻ MH $⊥$ Ox và MK $⊥$ Oy. Khi đó:

$\cos α = O H, \sin α = O K$

Xét tam giác OHK vuông tại O, ta có:

OH² + OK² = HK² (Py – ta – go)

Mà HK = OM = 1

⇒ OH² + OK² = 1

Hay $\cos^{2} α + \sin^{2} α = 1$ (đpcm).

b) Ta có:

$1 + \tan^{2} α = 1 + {(\frac{\sin α}{\cos α})}^{2} = 1 + \frac{\sin^{2} α}{{cos}^{2} α} = \frac{{cos}^{2} α + \sin^{2} α}{{cos}^{2} α} = \frac{1}{{cos}^{2} α} (α \neq 90^{0});$

c) Ta có:

1 + \cot^{2} α = 1 + {(\frac{c o s α}{\sin α})}^{2} = 1 + \frac{c o s^{2} α}{{sin}^{2} α} = \frac{{cos}^{2} α + \sin^{2} α}{{sin}^{2} α} = \frac{1}{{sin}^{2} α} (0^{0} < α < 180^{0});

Câu 2

Cho góc $α (0^{0} < α < 180^{0})$ thỏa mãn $\tan α = 3$ .

Tính giá trị của biểu thức: $P = \frac{2 \sin α - 3 c o s α}{3 \sin α + 2 c o s α} .$

Xem đáp án

Lời giải

Ta có: $1 + \tan^{2} α = \frac{1}{\cos^{2} α}$ (α ≠ 90^o)

$\Rightarrow \frac{1}{\cos^{2} α} = 1 + 3^{2} = 10$

$\Rightarrow \cos^{2} α = \frac{1}{10} \Leftrightarrow \cos α = \pm \frac{\sqrt{10}}{10}$

Vì 0^o < α < 180^o nên sin α > 0.

Mà tan α = 3 > 0 Þ cos α > 0 Þ $\cos α = \frac{\sqrt{10}}{10}$ .

Lại có: sin α = cos α . tan α = $3 . \frac{\sqrt{10}}{10} = \frac{3 \sqrt{10}}{10}$ .

Do đó $P = \frac{2 \sin α - 3 \cos α}{3 \sin α + 2 \cos α} = \frac{2 . \frac{3 \sqrt{10}}{10} - 3 . \frac{\sqrt{10}}{10}}{3 . \frac{3 \sqrt{10}}{10} + 2 . \frac{\sqrt{10}}{10}}$

$= \frac{\frac{\sqrt{10}}{10} (2 . 3 - 3)}{\frac{\sqrt{10}}{10} (3 . 3 + 2)} = \frac{3}{11}$

Vậy với α (0^o < α < 180^o) thỏa mãn tan α = 3 thì .

Câu 3

Không dùng bảng số hay máy tính cầm tay, tính giá trị của các biểu thức sau:

a) (2sin30⁰ + cos135⁰ – 3tan150⁰).(cos180⁰ – cot60⁰);

b) sin²90⁰ + cos²120⁰ + cos²0⁰ – tan²60⁰ + cot²135⁰;

c) cos60⁰.sin30⁰ + cos²30⁰.

Chú ý: $\sin^{2} α = {(\sin α)}^{2}, c o s^{2} α = {(c o s α)}^{2}, \tan^{2} α = {(\tan α)}^{2}, \cot^{2} α = {(\cot α)}^{2} .$

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

a) Nêu nhận xét về vị trí của điểm M trên nửa đường tròn đơn vị trong mỗi trường hợp sau:

$α = 90^{0};$

$α < 90^{0};$

$α > 90^{0};$

b) Khi $0^{0} < α < 90^{0}$ , nêu mối quan hệ giữa $c o s α, \sin α$ với hoành độ và tung độ của điểm M.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Trong Hình 3.6 hai điểm M, N ứng với hai góc phụ nhau $α$ và $90^{0} - α$ $(\hat{x O M} = α, \hat{x O N} = 90^{0} - α)$ . Chứng minh rằng ΔMOP = ΔNOQ. Từ đó nêu mối quan hệ giữa $\cos α$ và $\sin (90^{0} - α)$

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Đơn giản các biểu thức sau:

a) sin100⁰ + sin80⁰ + cos16⁰ + cos 164⁰;

b) $2 \sin (180^{0} - α) \cot α - c os (180^{0} - α) . \tan α . c os (180^{0} - α)$ với $0^{0} < α < 90^{0}$ .

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Hỏi bài tập

Đăng ký gói thi VIP

VIP +1 tháng ( 199,000 VNĐ )

VIP +1 - Luyện thi tất cả các đề có trên Website trong 1 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +3 tháng ( 299,000 VNĐ )

VIP +3 - Luyện thi tất cả các đề có trên Website trong 3 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +6 tháng ( 399,000 VNĐ )

VIP +6 - Luyện thi tất cả các đề có trên Website trong 6 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +12 tháng ( 499,000 VNĐ )

VIP +12 - Luyện thi tất cả các đề có trên Website trong 12 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

Bình luận

Chứng minh các hệ thức sau: a) sin2α+cos2α=1; b) 1+tan2α=1cos2αα≠900; c) 1+cot2α=1sin2α00<α<1800.

Cho góc α00<α<1800 thỏa mãn tanα=3. Tính giá trị của biểu thức: P=2sinα−3cosα3sinα+2cosα.

a) Nêu nhận xét về vị trí của điểm M trên nửa đường tròn đơn vị trong mỗi trường hợp sau: α=900; α<900; α>900; b) Khi 00<α<900, nêu mối quan hệ giữa cosα,sinαvới hoành độ và tung độ của điểm M.

Trong Hình 3.6 hai điểm M, N ứng với hai góc phụ nhau α và 900−αxOM^=α,xON^=900−α. Chứng minh rằng ΔMOP = ΔNOQ. Từ đó nêu mối quan hệ giữa cosα và sin900−α

Đơn giản các biểu thức sau: a) sin1000 + sin800 + cos160 + cos 1640; b) 2sin1800−αcotα−cos1800−α.tanα.cos1800−α với 00<α<900.

VIP +1 tháng ( 199,000 VNĐ )

VIP +3 tháng ( 299,000 VNĐ )

VIP +6 tháng ( 399,000 VNĐ )

VIP +12 tháng ( 499,000 VNĐ )

🔥 Đề thi HOT:

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đăng ký

Đăng nhập

Quên mật khẩu

Chứng minh các hệ thức sau:

a) $\sin^{2} α + \cos^{2} α = 1;$

b) $1 + \tan^{2} α = \frac{1}{{cos}^{2} α} (α \neq 90^{0});$

c) $1 + \cot^{2} α = \frac{1}{\sin^{2} α} (0^{0} < α < 180^{0}) .$

Cho góc $α (0^{0} < α < 180^{0})$ thỏa mãn $\tan α = 3$ .

Tính giá trị của biểu thức: $P = \frac{2 \sin α - 3 c o s α}{3 \sin α + 2 c o s α} .$

Trong Hình 3.6 hai điểm M, N ứng với hai góc phụ nhau $α$ và $90^{0} - α$ $(\hat{x O M} = α, \hat{x O N} = 90^{0} - α)$ . Chứng minh rằng ΔMOP = ΔNOQ. Từ đó nêu mối quan hệ giữa $\cos α$ và $\sin (90^{0} - α)$

Đơn giản các biểu thức sau:

a) sin100⁰ + sin80⁰ + cos16⁰ + cos 164⁰;

b) $2 \sin (180^{0} - α) \cot α - c os (180^{0} - α) . \tan α . c os (180^{0} - α)$ với $0^{0} < α < 90^{0}$ .