Bài tập Bài 17. Dấu của tam thức bậc hai có đáp án

Hướng dẫn giải

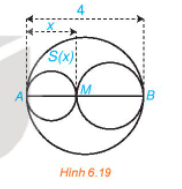
Theo Bài 16, diện tích mảnh đất được rào chắn là S(x) = – 2x² + 20x (m²).

Vì mảnh đất được rào chắn có diện tích không nhỏ hơn 48 m² nghĩa là S(x) phải lớn hơn hoặc bằng 48.

Khi đó: – 2x² + 20x ≥ 48 ⇔ 2x² – 20x + 48 ≤ 0 (1).

Ta cần giải bất phương trình (1).

Sau bài học này ta sẽ giải được bất phương trình (1) như sau:

Tam thức bậc hai f(x) = 2x² – 20x + 48 có hai nghiệm x₁ = 4; x₂ = 6 và hệ số a = 2 > 0. Từ đó suy ra tập nghiệm của bất phương trình (1) là đoạn [4; 6]. Như vậy khoảng cách từ điểm cắm cột đến bờ tường phải lớn hơn hoặc bằng 4 m và nhỏ hơn hoặc bằng 6 m thì mảnh đất rào chắn của bác Việt sẽ có diện tích không nhỏ hơn 48 m².

Hướng dẫn giải

Ta có: A = 0,5x² = 0,5x² + 0x + 0;

B = 1 – x² = – x² + 0x + 1;

C = x² + x + 1;

D = (1 – x)(2x + 1) = 2x + 1 – 2x² – x = – 2x² + x + 1.

Các biểu thức trên đều có dạng ax² + bx + c, trong đó a, b, c là các số thực và a ≠ 0.

Hướng dẫn giải

Trong các biểu thức A, B, C, D trên, chỉ có biểu thức C = \( - \frac{2}{3}{x^2} + 7x - 4\) là tam thức bậc hai vì nó có dạng ax² + bx + c, trong đó a = \( - \frac{2}{3}\), b = 7, c = – 4 là các số thực và a ≠ 0.

Hướng dẫn giải

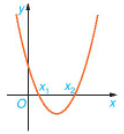
a) Hàm số bậc hai y = f(x) = x² – 4x + 3.

Hệ số a = 1 > 0.

Ta có: f(0) = 0² – 4 . 0 + 3 = 3 > 0, f(0) cùng dấu với hệ số a.

f(1) = 1² – 4 . 1 + 3 = 0, f(1) không mang dấu.

f(2) = 2² – 4 . 2 + 3 = – 1 < 0, f(2) trái dấu với hệ số a.

f(3) = 3² – 4 . 3 + 3 = 0, f(3) không mang dấu.

f(4) = 4² – 4 . 4 + 3 = 3 > 0, f(4) cùng dấu với hệ số a.

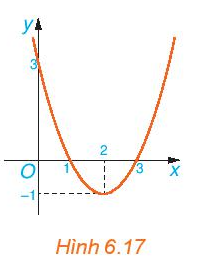
b) Quan sát đồ thị H.6.17, ta thấy:

+ Trên các khoảng (– ∞; 1) và (3; +∞), đồ thị hàm số nằm hoàn toàn phía trên trục Ox.

+ Trên khoảng (1; 3), đồ thị hàm số nằm hoàn toàn phía dưới trục Ox.

c) Khi đồ thị hàm số nằm hoàn toàn trên trục Ox thì f(x) > 0, ngược lại khi đồ thị hàm số nằm hoàn toàn phía dưới trục Ox thì f(x) < 0.

Hệ số a = 1 > 0.

Vậy trên các khoảng (– ∞; 1) và (3; +∞), f(x) cùng dấu với hệ số a; trên khoảng (1; 3), f(x) trái dấu với hệ số a.

Hướng dẫn giải

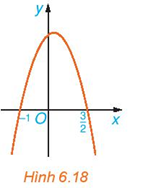
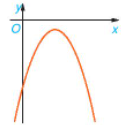
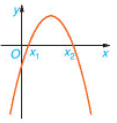
a) Quan sát đồ thị ta thấy:

+ Trên các khoảng (– ∞; – 1) và \(\left( {\frac{3}{2}; + \infty } \right)\), đồ thị nằm hoàn toàn phía dưới trục Ox.

+ Trên khoảng \(\left( { - 1;\frac{3}{2}} \right)\), đồ thị nằm hoàn toàn phía trên trục Ox.

b) Khi đồ thị hàm số nằm hoàn toàn trên trục Ox thì g(x) > 0, ngược lại khi đồ thị hàm số nằm hoàn toàn phía dưới trục Ox thì g(x) < 0.

Hệ số a = – 2 < 0, do đó ta có:

+ Trên các khoảng (– ∞; – 1) và \(\left( {\frac{3}{2}; + \infty } \right)\), g(x) cùng dấu với hệ số a.

+ Trên khoảng \(\left( { - 1;\frac{3}{2}} \right)\), g(x) trái dấu với hệ số a.