Bài tập Vecto trong mặt phẳng tọa độ có đáp án
32 người thi tuần này 4.6 1.9 K lượt thi 14 câu hỏi
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề kiểm tra Thực hành tính xác suất theo định nghĩa cổ điển (có lời giải) - Đề 3
Đề kiểm tra Thực hành tính xác suất theo định nghĩa cổ điển (có lời giải) - Đề 2
Đề kiểm tra Thực hành tính xác suất theo định nghĩa cổ điển (có lời giải) - Đề 1
Đề kiểm tra Biến cố và định nghĩa cổ điển của xác suất (có lời giải) -Đề 2
Đề kiểm tra Biến cố và định nghĩa cổ điển của xác suất (có lời giải) -Đề 2
Danh sách câu hỏi:
Lời giải
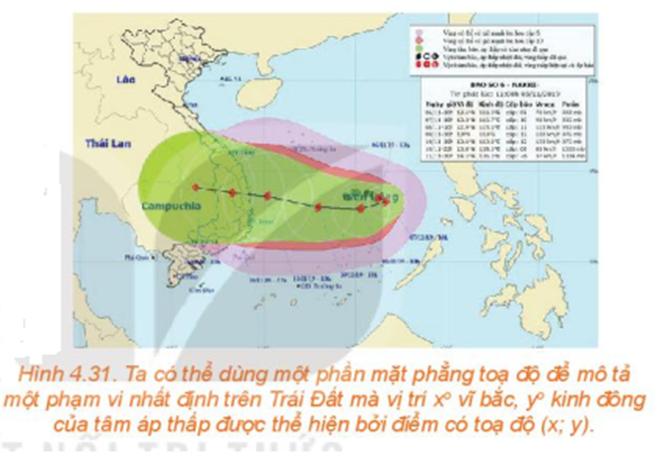
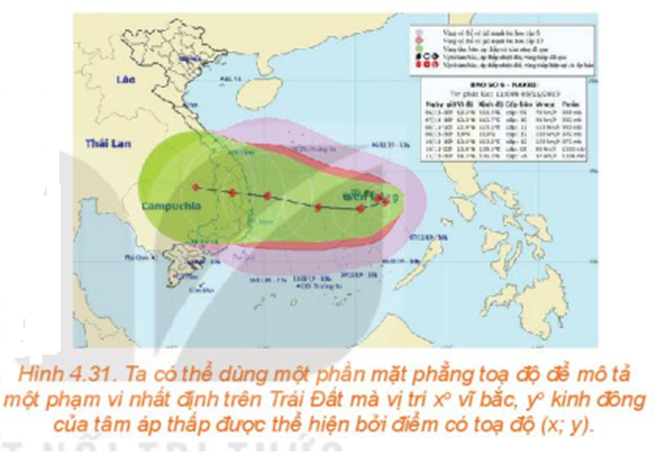
Gọi M(x; y) là vị trí của tâm bão tại thời điểm bất kì t giờ trong khoảng thời gian 12 giờ.
Do bão di chuyển thẳng đều từ A(13,8; 108,3) tới vị trí có tọa độ B(14,1; 106,3) nên điểm M thuộc đoạn thẳng AB.
Theo dự báo, tại thời điểm t giờ thì tâm bão đã đi được một khoảng AM là:
Hay
Vectơ cùng hướng với vectơ và nên
Ta có: A(13,8; 108,3); B(14,1; 106,3); M(x; y)
Suy ra
Ta có:
Vậy ở thời điểm t giờ tâm bão là điểm M ở vị trí
Lời giải
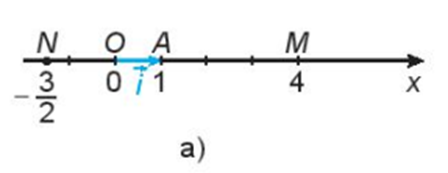
Ta có vecto cùng hướng với vectơ và OM = 4OA nên ta có .
Ta có vecto ngược hướng với vectơ và ON = OA nên ta có .
Lời giải
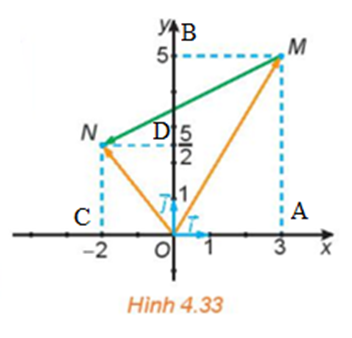
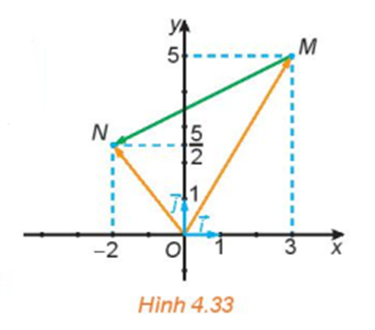
a) Xét hình bình hành OAMB, có:
(quy tắc hình bình hành)
Xét hình bình hành OCND, có:
(quy tắc hình bình hành)
b) Xét tam giác OMN, có:
(quy tắc ba điểm)
Lời giải
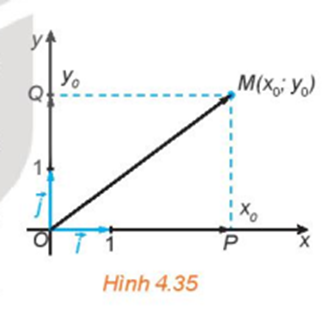
Ta có: .
Vậy tọa độ của là
Lời giải
a) Ta có:
b) Ta có:
c) Ta có .
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.