(Phương trình đoạn chắn của đường thẳng)

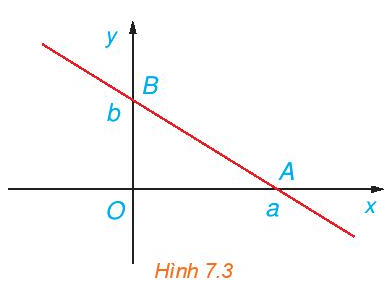
Chứng minh rằng, đường thẳng đi qua hai điểm A(a; 0), B(0; b) với ab ≠ 0 (H.7.3) có phương trình là \(\frac{x}{a} + \frac{y}{b} = 1\).

Hướng dẫn giải

a) Tại sân bay Nội Bài, máy bay bắt đầu bay ứng với thời gian t = 0.

Tọa độ của sân bay Đà Nẵng thỏa mãn hệ \(\left\{ \begin{array}{l}x = 21,2 - \frac{{153}}{{40}}t\\y = 105,8 + \frac{9}{5}t\end{array} \right.\).

Do đó, thời gian máy bay bay từ Hà Nội đến Đà Nẵng là nghiệm t của hệ \(\left\{ \begin{array}{l}16,1 = 21,2 - \frac{{153}}{{40}}t\,\,\,\,\,\,\,\,\,\left( 1 \right)\\108,2 = 105,8 + \frac{9}{5}t\,\,\,\,\,\,\,\left( 2 \right)\end{array} \right.\).

Từ (1) suy ra t = \(\frac{4}{3}\).

Từ (2) suy ra t = \(\frac{4}{3}\).

Do đó t = \(\frac{4}{3}\) là nghiệm của hệ trên.

Vậy chuyến bay từ Hà Nội đến Đà Nẵng mất \(\frac{4}{3}\) giờ.

b) Tại thời điểm 1 giờ kể từ lúc cất cánh, nghĩa là t = 1, thay vào hệ \(\left\{ \begin{array}{l}x = 21,2 - \frac{{153}}{{40}}t\\y = 105,8 + \frac{9}{5}t\end{array} \right.\) ta được: \(\left\{ \begin{array}{l}x = 21,2 - \frac{{153}}{{40}}.1\\y = 105,8 + \frac{9}{5}.1\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}x = 17,375\\y = 107,6\end{array} \right.\).

Do đó tại thời điểm 1 giờ kể từ lúc cất cánh, máy bay đang ở vị trí có 17,375° Bắc và có kinh độ 107,6° Đông.

Vậy tại thời điểm 1 giờ kể từ lúc cất cánh, máy bay chưa bay qua vĩ tuyến 17 (17° Bắc).

Hai trục tọa độ vuông góc với nhau nên vectơ chỉ phương của trục này là vectơ pháp tuyến của trục kia.