Một lớp có 40 học sinh trong đó có 16 nam. Trong các em nam có 3 em thuận tay trái. Trong các em nữ có 2 em thuận tay trái. Chọn ngẫu nhiên hai em. Tính xác suất để hai em chọn được có một em nữ không thuận tay trái và một em nam thuận tay trái.
Một lớp có 40 học sinh trong đó có 16 nam. Trong các em nam có 3 em thuận tay trái. Trong các em nữ có 2 em thuận tay trái. Chọn ngẫu nhiên hai em. Tính xác suất để hai em chọn được có một em nữ không thuận tay trái và một em nam thuận tay trái.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Số cách để chọn ngẫu nhiên hai em trong 40 em học sinh là: = 780 (cách).
Do đó, ta có n(Ω) = 780.
Gọi A là biến cố: “Hai em chọn được có một em nữ không thuận tay trái và một em nam thuận tay trái”
Lớp có 40 – 16 = 24 em nữ, trong đó, 24 – 2 = 22 em không thuận tay trái. Do đó, số cách chọn 1 em nữ không thuận tay trái là 22 cách.
Trong lớp có 3 em nam thuận tay trái, do đó, số cách chọn 1 em nam thuận tay trái là 3 cách.
Theo quy tắc nhân ta có: n(A) = 22 . 3 = 66.
Vậy xác suất của biến cố A là: P(A) = .
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
a)
Kí hiệu Đ, X, V tương ứng là viên bi màu đỏ, xanh, vàng.
Ta có sơ đồ hình cây mô tả các phần tử của không gian mẫu:
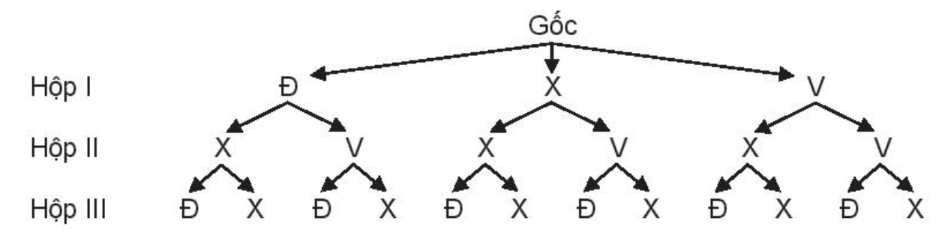
Do đó, ta có:
Ω = {(ĐXĐ; ĐXX; ĐVĐ; ĐVX; XXĐ; XXX; XVĐ; XVX; VXĐ; VXX; VVĐ; VVX}.
Vậy n(Ω) = 12.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Gọi a là số trên thẻ rút được từ hộp I, a ∈ {1; 2; 3}.
Gọi b là số trên thẻ rút được từ hộp II, b ∈ {2; 4; 6; 8}.
Gọi c là số trên thẻ rút được từ hộp III, c ∈ {1; 3; 5; 7; 9; 11}.
Ta có không gian mẫu: Ω = {(a, b, c) | a ∈ {1; 2; 3}, b ∈ {2; 4; 6; 8}, c ∈ {1; 3; 5; 7; 9; 11}}.
Theo quy tắc nhân, ta có: n(Ω) = 3 . 4 . 6 = 72.
Xét biến cố A: “Tổng ba số trên ba tấm thẻ là số lẻ”.
Do b luôn là một số chẵn và c luôn là một số lẻ nên tổng b + c luôn là một số lẻ, do đó để (a + b + c) là một số lẻ thì a phải là số chẵn. Do đó, a = 2.
Khi đó, A = {(2, b, c) | b ∈ {2; 4; 6; 8}, c ∈ {1; 3; 5; 7; 9; 11}}.
Do đó, n(A) = 1 . 4 . 6 = 24.
Vậy P(A) =
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập