b) Tính xác suất để:
• Tất cả đều vào một quán;
• Mỗi quán có đúng 2 bạn vào;
• Quán A có 3 bạn vào, quán B có 1 bạn vào;
• Một quán có 3 bạn vào, quán kia có 1 bạn vào.
b) Tính xác suất để:
• Tất cả đều vào một quán;
• Mỗi quán có đúng 2 bạn vào;
• Quán A có 3 bạn vào, quán B có 1 bạn vào;
• Một quán có 3 bạn vào, quán kia có 1 bạn vào.
Quảng cáo
Trả lời:
b)
Ta có không gian mẫu:
Ω = {AAAA; AAAB; AABA; AABB; ABAA; ABAB; ABBA; ABBB; BAAA; BAAB; BABA; BABB; BBAA; BBAB; BBBA; BBBB}.
Do đó, n(Ω) = 16.
Gọi biến cố E: “Tất cả đều vào một quán”. Ta có:
E = {AAAA; BBBB}, n(E) = 2, suy ra P(E) =
Gọi biến cố F: “Mỗi quán có đúng hai bạn vào”. Ta có:
F = {AABB; ABAB; ABBA; BAAB; BABA; BBAA}, n(F) = 6,
suy ra P(F) =
Gọi biến cố G: “Quán A có 3 bạn vào, quán B có 1 bạn vào”. Ta có:
G = {AAAB; AABA; ABAA; BAAA}, n(G) = 4, suy ra P(G) =
Gọi biến cố K: “Một quán có 3 bạn vào, quán kia có 1 bạn vào.”. Ta có:
K1: “Quán A có 3 bạn vào, quán B có 1 bạn vào” nên K1 = G, n(K1) = 4.
K2: “Quán B có 3 bạn vào, quán A có 1 bạn vào”. Ta có:
K2 = {BBBA; BBAB; BABB; ABBB}, n(K2) = 4
n(K) = n(K1) + n(K2) = 4 + 4 = 8.
Vậy P(K) =
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Sách - Sổ tay kiến thức trọng tâm Vật lí 10 VietJack - Sách 2025 theo chương trình mới cho 2k9 ( 31.000₫ )
- Trọng tâm Lí, Hóa, Sinh 10 cho cả 3 bộ KNTT, CTST và CD VietJack - Sách 2025 ( 40.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Số cách để chọn ngẫu nhiên hai em trong 40 em học sinh là: = 780 (cách).
Do đó, ta có n(Ω) = 780.
Gọi A là biến cố: “Hai em chọn được có một em nữ không thuận tay trái và một em nam thuận tay trái”
Lớp có 40 – 16 = 24 em nữ, trong đó, 24 – 2 = 22 em không thuận tay trái. Do đó, số cách chọn 1 em nữ không thuận tay trái là 22 cách.
Trong lớp có 3 em nam thuận tay trái, do đó, số cách chọn 1 em nam thuận tay trái là 3 cách.
Theo quy tắc nhân ta có: n(A) = 22 . 3 = 66.
Vậy xác suất của biến cố A là: P(A) = .
Lời giải
a)
Kí hiệu Đ, X, V tương ứng là viên bi màu đỏ, xanh, vàng.
Ta có sơ đồ hình cây mô tả các phần tử của không gian mẫu:
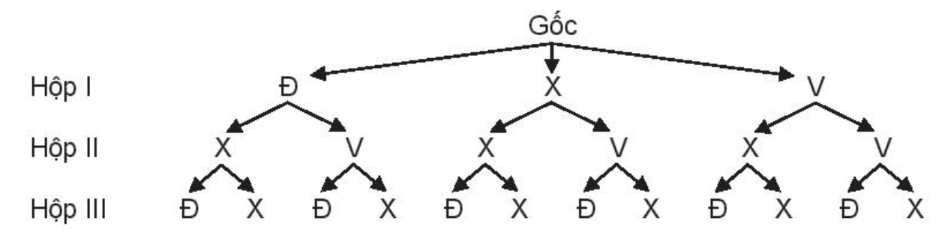
Do đó, ta có:
Ω = {(ĐXĐ; ĐXX; ĐVĐ; ĐVX; XXĐ; XXX; XVĐ; XVX; VXĐ; VXX; VVĐ; VVX}.
Vậy n(Ω) = 12.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.