Câu hỏi:
11/07/2024 4,414Cho hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) thoả mãn \(\left| {\overrightarrow a } \right| = 6,\left| {\overrightarrow b } \right| = 8\) và \(\left| {\overrightarrow a + \overrightarrow b } \right| = 10.\)
Tính số đo của góc giữa hai vectơ \(\overrightarrow a \) và \(\overrightarrow a + \overrightarrow b .\)
Quảng cáo
Trả lời:
Giải bởi Vietjack
Lời giải
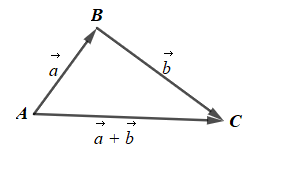
Gọi ba điểm A, B, C sao cho \(\overrightarrow {AB} = \overrightarrow a ,\overrightarrow {BC} = \overrightarrow b \)
Khi đó \(\overrightarrow a + \overrightarrow b = \overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \)
Và AB = 6, BC = 8 và AC = 10.
Xét tam giác ABC có:
• AB2 + BC2 = 62 + 82 =100
AC2 = 102 = 100
AB2 + BC2 = AC2
Do đó tam giác ABC vuông tại B (định lí Pythagore đảo)
• \(cos\widehat {BAC} = \frac{{AB}}{{AC}} = \frac{6}{{10}} = \frac{3}{5}\)
\(cos\left( {\overrightarrow a ;\overrightarrow a + \overrightarrow b } \right) = cos\widehat {BAC} = \frac{3}{5}\)
\[ \Rightarrow \widehat {BAC} \approx 53^\circ 7'48''\]
Vậy \(\left( {\overrightarrow a ;\overrightarrow a + \overrightarrow b } \right) \approx 53^\circ 7'48''.\)
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
- Sách - Sổ tay kiến thức trọng tâm Vật lí 10 VietJack - Sách 2025 theo chương trình mới cho 2k9 ( 31.000₫ )
- Trọng tâm Toán, Văn, Anh 10 cho cả 3 bộ KNTT, CTST, CD VietJack - Sách 2025 ( 13.600₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Lời giải
Vì tam giác ABC vuông tại A nên AB ⊥ AC hay \(\overrightarrow {AB} \bot \overrightarrow {AC} \)
Do đó \(\overrightarrow {AB} .\overrightarrow {AC} = 0\)
Giả sử C(x; 0) là điểm thuộc trục hoành.
Với A(2; 1), B(4; 3) và C(x; 0) ta có:
\(\overrightarrow {AB} = \left( {2;2} \right)\) và \(\overrightarrow {AC} = \left( {x - 2; - 1} \right)\)
Khi đó \(\overrightarrow {AB} .\overrightarrow {AC} = 0\) 2(x – 2) + 2(–1) = 0
2x – 4 – 2 = 0
2x = 6
x = 3
Vậy C(3; 0).
\( \Rightarrow \overrightarrow {AC} = \left( {1; - 1} \right)\)
Ta có:
• \(\overrightarrow {AB} = \left( {2;2} \right) \Rightarrow AB = \sqrt {{2^2} + {2^2}} = 2\sqrt 2 \)
• \(\overrightarrow {AC} = \left( {1; - 1} \right) \Rightarrow AC = \sqrt {{1^2} + {{\left( { - 1} \right)}^2}} = \sqrt 2 \)
• \(BC = \sqrt {A{B^2} + A{C^2}} = \sqrt {{{\left( {2\sqrt 2 } \right)}^2} + {{\left( {\sqrt 2 } \right)}^2}} = \sqrt {10} \) (theo định lí Pythagore)
Khi đó chu vi tam giác ABC là:
AB + AC + BC = \(2\sqrt 2 + \sqrt 2 + \sqrt {10} = 3\sqrt 2 + \sqrt {10} \)(đơn vị độ dài)
Diện tích tam giác ABC là:
\(\frac{1}{2}.AB.AC = \frac{1}{2}.2\sqrt 2 .\sqrt 2 = 2\) (đơn vị diện tích)
Lời giải
Lời giải
Với A(–3; 2), B(1; 5) và C(3; −1) ta có:
\(\overrightarrow {AB} = \left( {4;3} \right)\)và \(\overrightarrow {AC} = \left( {6; - 3} \right)\)
Vì \(\frac{4}{6} = \frac{2}{3} \ne \frac{3}{{ - 3}} = - 1\) nên hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {AC} \) không cùng phương
Do đó ba điểm A, B, C không thẳng hàng
Vậy A, B, C là ba đỉnh của một tam giác.
Vì G là trọng tâm của tam giác ABC nên ta có:
\(\left\{ \begin{array}{l}{x_G} = \frac{{ - 3 + 1 + 3}}{3} = \frac{1}{3}\\{y_G} = \frac{{2 + 5 + \left( { - 1} \right)}}{3} = 2\end{array} \right.\) \( \Rightarrow G\left( {\frac{1}{3};2} \right)\)
Vậy tọa độ trọng tâm của tam giác ABC là: \(G\left( {\frac{1}{3};2} \right)\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
13 câu Trắc nghiệm Tích của vectơ với một số có đáp án (Thông hiểu)
-
12 Bài tập Ứng dụng của hàm số bậc hai để giải bài toán thực tế (có lời giải)
-
16 câu Trắc nghiệm Toán 10 Kết nối tri thức Mệnh đề có đáp án
-
10 Bài tập Ứng dụng ba đường conic vào các bài toán thực tế (có lời giải)
-
10 Bài tập Tìm hệ số, số hạng trong khai triển nhị thức Newton (có lời giải)
-
10 Bài tập Cách xét tính đúng sai của mệnh đề (có lời giải)
-
10 Bài tập Cách xét tính đúng sai của mệnh đề (có lời giải)
-
10 Bài tập Tính số trung bình, trung vị, tứ phân vị và mốt của mẫu số liệu cho trước (có lời giải)
Nhắn tin Zalo