Câu hỏi:
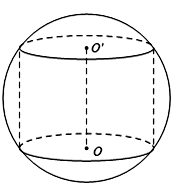
27/06/2022 247Cho khối cầu \(\left( S \right)\) tâm I, bán kính R không đổi. Một khối trụ thay đổi có chiều cao h và bán kính đáy r nội tiếp khối cầu. Tính chiều cao h theo R sao cho thể tích của khối trụ lớn nhất.
Câu hỏi trong đề: Bộ đề minh họa môn Toán THPT Quốc gia năm 2022 (30 đề) !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án A
Gọi r, h lần lượt là bán kính đáy và chiều cao của khối trụ.
Vì khối trụ nội tiếp khối cầu \( \Rightarrow {R^2} = {r^2} + {\left( {\frac{h}{2}} \right)^2} \Leftrightarrow {r^2} = {R^2} - \frac{{{h^2}}}{4}\).
Thể tích của khối trụ là \(V = \pi {r^2}h = \pi h\left( {{R^2} - \frac{{{h^2}}}{4}} \right) = \frac{\pi }{4}.h\left( {4{{\rm{R}}^2} - {h^2}} \right)\).
Xét hàm số \(f\left( h \right) = 4{{\rm{R}}^2}h - {h^3}\) với \(h \in \left( {0;2{\rm{R}}} \right)\), có \(f'\left( h \right) = 4{{\rm{R}}^2} - 3{h^2} = 0 \Leftrightarrow h = \frac{{2R}}{{\sqrt 3 }}\).
Lập bảng biến thiên, ta được \(f\left( h \right)\) đạt GTLN khi và chỉ khi \(h = \frac{{2{\rm{R}}\sqrt 3 }}{3}\).
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án D
Đặt \(t = 2{\rm{x}} \Rightarrow dt = 2{\rm{dx}}\). Đổi cận \(x = 0 \Rightarrow t = 0,{\rm{ }}x = 3 \Rightarrow t = 6\).
\(\int\limits_0^3 {f\left( {2{\rm{x}}} \right)d{\rm{x}}} = \frac{1}{2}\int\limits_0^6 {f\left( t \right)dt} = \frac{1}{2}\int\limits_0^6 {f\left( x \right)d{\rm{x}}} = \frac{1}{2}.10 = 5\).
Lời giải
Đáp án A
Theo giả thiết ta có: \(\int\limits_{ - 2}^0 {\left| {f\left( x \right)} \right|d{\rm{x}}} = \int\limits_{ - 2}^0 { - f\left( x \right)d{\rm{x}}} = 1 \Rightarrow \int\limits_{ - 2}^0 {f\left( x \right)d{\rm{x}}} = - 1;{\rm{ }}\int\limits_0^3 {\left| {f\left( x \right)} \right|d{\rm{x}}} = \int\limits_0^3 {f\left( x \right)d{\rm{x}}} = 3\)
Do đó: \(\int\limits_{ - 2}^3 {f\left( x \right)d{\rm{x}}} = \int\limits_{ - 2}^0 {f\left( x \right)d{\rm{x}}} + \int\limits_0^3 {f\left( x \right)d{\rm{x}}} = - 1 + 3 = 2\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
30 Đề thi thử thpt quốc gia môn Toán có lời giải chi tiết mới nhất (Đề số 1)
-
CÂU TRẮC NGHIỆM ĐÚNG SAI
-
(2025 mới) Đề thi ôn tập THPT môn Toán có đáp án (Đề số 1)
-
Đề minh họa tốt nghiệp THPT môn Toán có đáp án năm 2025 (Đề 1)
-
Đề minh họa tốt nghiệp THPT môn Toán có đáp án năm 2025 (Đề 2)
-
Đề minh họa tốt nghiệp THPT môn Toán có đáp án năm 2025 (Đề 19)
-
(2025 mới) Đề thi ôn tập THPT môn Toán có đáp án (Đề số 2)
-
45 bài tập Xác suất có lời giải