Câu hỏi:
12/07/2024 906
Theo bảng giá trị dưới đây, hai đại lượng x và y có phải là hai đại lượng tỉ lệ nghịch không?
a)
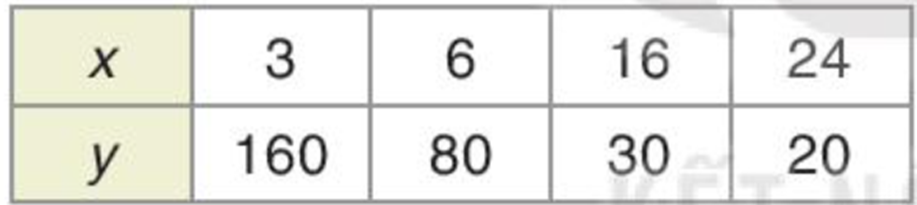
b)
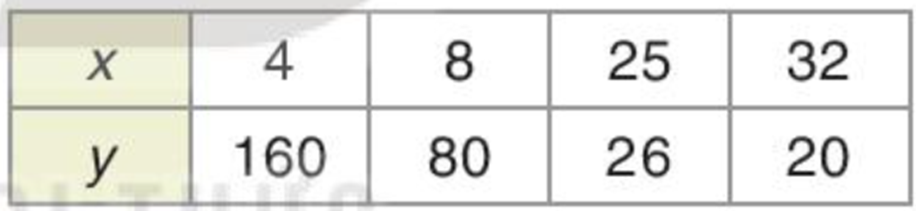
Theo bảng giá trị dưới đây, hai đại lượng x và y có phải là hai đại lượng tỉ lệ nghịch không?
a)
b)
Câu hỏi trong đề: Bài tập Bài 23. Đại lượng tỉ lệ nghịch có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Lời giải:
a) Ta thấy 3.160 = 480; 6.80 = 480; 16.30 = 480; 24.20 = 480.
Do đó x.y = 480.
Vậy x và y là hai đại lượng tỉ lệ nghịch.
b) Ta thấy 4.160 = 640; 8.80 = 640; 25.26 = 650; 32.20 = 640.
Do 640 ≠ 650 nên x và y không phải hai đại lượng tỉ lệ nghịch.
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Lời giải:
Gọi số máy cày của ba đội lần lượt là x, y, z (máy cày).
Do đội thứ nhất hoàn thành công việc trong 4 ngày, đội thứ hai trong 6 ngày và đội thứ ba trong 8 ngày nên 4x = 6y = 8z hay .
Do số máy của đội thứ nhất nhiều hơn số máy của đội thứ hai là 2 máy nên x - y = 2.
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
Do đó x = 1/4.24 = 6; y = 1/6.24 = 4; z = 1/8.24 = 3.
Vậy số máy cày của đội thứ nhất, thứ hai, thứ ba lần lượt là 6 máy, 4 máy và 3 máy.
Lời giải
Lời giải:
Gọi x, y, z (quyển vở) lần lượt là số quyển vở loại 120 trang, 200 trang và 240 trang.
Bạn An mua tổng cộng 34 quyển nên ta có x + y + z = 34.
Do số tiền An dành để mua mỗi loại vở là như nhau nên 12x = 18y = 20z.
Do đó .
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
.
Do đó x = 1/2.180 = 15; y = 1/18.180 = 10; z = 1/20.180 = 9.
Vậy số vở An mua của ba loại 120 trang, 200 trang và 240 trang lần lượt là 15 quyển, 10 quyển và 9 quyển.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Đề kiểm tra cuối học kỳ 2 Toán 7 Kết nối tri thức có đáp án - Đề 1
-
Bộ 7 đề thi học kì 2 Toán lớp 7 Chân trời sáng tạo có đáp án - Đề 04
-
15 câu Trắc nghiệm Toán 7 Kết nối tri thức Bài 1: Tập hợp các số hữu tỉ có đáp án
-
15 câu Trắc nghiệm Toán 7 Cánh diều Bài 1: Tập hợp Q các số hữu tỉ có đáp án
-
Đề kiểm tra cuối học kỳ 2 Toán 7 Kết nối tri thức có đáp án - Đề 2
-
15 câu Trắc nghiệm Toán 7 Chân trời sáng tạo Bài 1: Tập hợp các số hữu tỉ có đáp án
-
Bộ 15 đề thi Học kì 2 Toán 7 có đáp án (Mới nhất) - đề 2
-
Bộ 10 đề thi giữa kì 1 Toán 7 Kết nối tri thức cấu trúc mới có đáp án - Đề 1
Nhắn tin Zalo