Trong mặt phẳng, cho 6 đường thẳng song song và 8 đường thẳng song song cùng vuông góc với 6 đường thẳng đó. Có bao nhiêu hình chữ nhật được tạo thành?
Câu hỏi trong đề: Bài tập Cuối chương 5 có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hướng dẫn giải
Cứ 2 đường thẳng trong nhóm 6 đường thẳng song song và 2 đường thẳng trong nhóm 8 đường thẳng song song cùng vuông góc với 6 đường thẳng trên tạo thành 1 hình chữ nhật.
Do đó, việc lập một hình chữ nhật được thực hiện bởi 2 hành động liên tiếp sau:
+ Chọn 2 đường thẳng trong 6 đường thẳng có \(C_6^2 = 15\) cách chọn.
+ Chọn 2 đường thẳng trong 8 đường thẳng có \(C_8^2 = 28\) cách chọn.
Theo quy tắc nhân, số hình chữ nhật được tạo thành là: 15 . 28 = 420 (hình chữ nhật).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Hướng dẫn giải
Theo bài ra ta vẽ được sơ đồ hình cây như sau:
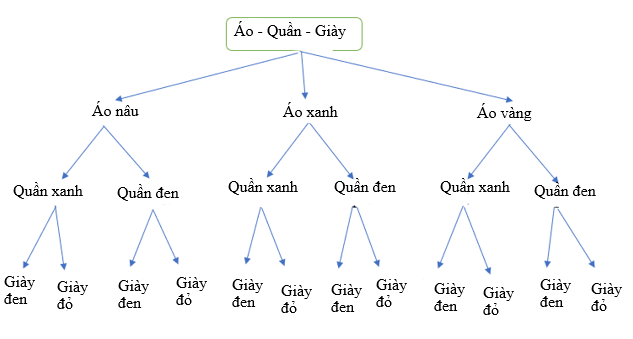
Từ sơ đồ ta thấy, có 12 cách chọn một bộ quần áo và một đôi giày cho bạn Dương.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Hướng dẫn giải
Để lập một mật khẩu máy tính gồm 8 kí tự, ta cần thực hiện liên tiếp các hành động sau:
+ Chọn 4 kí tự đầu tiên bằng cách lập 4 chữ số đôi một khác nhau trong 10 chữ số, vì có kể thứ tự, nên có \(A_{10}^4 = 5040\) cách lập.
+ Chọn 2 kí tự tiếp theo là chữ cái in thường, vì 2 kí tự này không nhất thiết khác nhau, nên ta chọn lần lượt từng kí tự, kí tự chữ in thường thứ nhất chọn 1 trong 26, có 26 cách chọn, tương tự có 26 cách chọn kí tự chữ in thường thứ hai. Do đó, chọn 2 kí tự tiếp theo là chữ in thường có 26 . 26 = 676 cách chọn.
+ Chọn 1 kí tự tiếp theo là chữ cái in hoa, chọn 1 chữ trong 26 chữ có 26 cách chọn.
+ Chọn 1 kí tự cuối cùng là kí tự đặc biệt, chọn 1 trong 10 kí tự đặc biệt có 10 cách chọn.
Theo quy tắc nhân, vậy số cách lập một mật khẩu máy tính của bạn Ngân là:
5040 . 676 . 26 . 10 = 885 830 400 (cách lập).
Vậy bạn Ngân có 885 830 400 cách lập một mật khẩu máy tính.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập