Cho: xy + z + t=yx + t + z=zx + y + t=tx + y + z Tính Q = x + yz + t + y + zx + t + z + tx + y + t + xz + y

Từ xy + z + t=yx + t + z=zx + y + t=tx + y + z => xy + z + t+1=yx + t + z+1=zx + y + t+1=tx + y + z+1 => x + y + z + ty + z + t=y + z + x + tx + t + z=z + x + t + yx + y + t=t + x + y + zx + y + z(*) +) Nếu x + y + z + t = 0 => x + y = –(z + t) ; y + z = – (x + t) ; z + t = – (x + y) ; t + x = – (y + z) Q = –1 –1 –1 –1 = –4 (0,5 điểm) +) Nếu x + y + z + t 0 từ (*) y + z + t = x + t + z = x + y + t = x + y + z x = y = t = z Từ đó tính Q = 1 + 1 + 1 + 1 = 4 (0,5 điểm)

Câu hỏi:

06/07/2022 171

Cho: $\frac{x}{y + z + t} = \frac{y}{x + t + z} = \frac{z}{x + y + t} = \frac{t}{x + y + z}$

Tính Q = $\frac{x + y}{z + t} + \frac{y + z}{x + t} + \frac{z + t}{x + y} + \frac{t + x}{z + y}$

Xem lời giải

Câu hỏi trong đề: Bộ 15 đề thi Học kì 2 Toán 7 có đáp án (Mới nhất) !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Từ $\frac{x}{y + z + t} = \frac{y}{x + t + z} = \frac{z}{x + y + t} = \frac{t}{x + y + z}$

=> $\frac{x}{y + z + t} +1= \frac{y}{x + t + z} +1= \frac{z}{x + y + t} +1= \frac{t}{x + y + z} + 1$

=> $\frac{x + y + z + t}{y + z + t} = \frac{y + z + x + t}{x + t + z} = \frac{z + x + t + y}{x + y + t} = \frac{t + x + y + z}{x + y + z}$ (*)

+) Nếu x + y + z + t = 0

=> x + y = –(z + t) ; y + z = – (x + t) ; z + t = – (x + y) ; t + x = – (y + z)

Q = –1 –1 –1 –1 = –4 (0,5 điểm)

+) Nếu x + y + z + t 0 từ (*) y + z + t = x + t + z = x + y + t = x + y + z

x = y = t = z

Từ đó tính Q = 1 + 1 + 1 + 1 = 4 (0,5 điểm)

Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Cho $ΔABC$ vuông tại A, kẻ tia phân giác của $\hat{ABC}$ cắt AC tại D. Kẻ DE vuông góc với BC tại E, gọi F là giao điểm của BA và ED .

          a) Chứng minh $Δ ABD = Δ EBD$ ;

          b) So sánh AD và DC;

          c) Gọi K là trung điểm của FC. Chứng minh ba điểm B; D; K thẳng hàng.

Xem đáp án

Lời giải

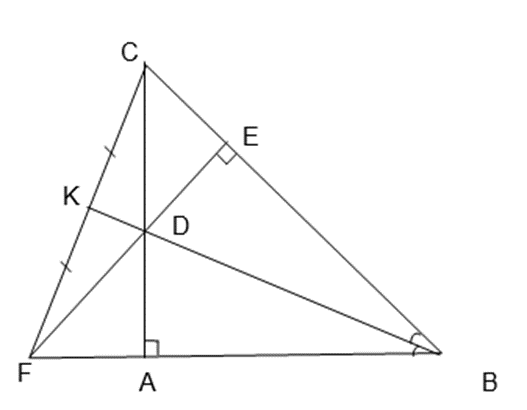
Cho vuông tại A, kẻ tia phân giác của cắt AC tại D. Kẻ DE vuông góc với BC tại E, gọi F là giao điểm của BA và ED . a) Chứng minh ; b) So sánh AD và DC; c) Gọi K là trung điểm của FC. Chứng minh ba điểm B; D; K thẳng hàng. (ảnh 1)

a) Chứng minh $ΔABD = ΔEBD$

Xét tam giác ABD và tam giác EBD có:

$\hat{ADB} = \hat{DEB} {= 90}^{0}$

Cạnh DB chung

$\hat{ABD} = \hat{EBD}$ $(V ì B D l à t i a p h â n g i á c c ủ a ABC)$

Do đó:

ΔABD = ΔEBD

(cạnh huyền - góc nhọn)

b, So sánh AD và DC.

Vì

ΔABD = ΔEBD

(c/m trên) AD = ED (Cạnh tương ứng)

T a m g i á c D E C v u ô n g t ạ i E

D C > D E (T r o n g t a m g i á c v u ô n g c ạ n h h u y ề n l à c ạ n h l ớ n n h ấ t) D o đ ó : D C > A D

Chứng minh ba điểm B; D; K thẳng hàng

Ta có BD là tia phân giác của

\hat{ABC}

(GT)

Ta có: $\hat{C D E} = \hat{F D A}$ (hai góc đối đỉnh)

$\hat{E D B} = \hat{A D B}$ $ΔABD = ΔEBD$

Suy ra: $\hat{C D E} + \hat{E D B} = \hat{F D A} + \hat{A D B}$ $\Rightarrow \hat{C D B} = \hat{F D B}$

Xét tam giác FDB và tam giác CDB có:

$\hat{C D B} = \hat{F D B} (c m t)$

DB cạnh chung

$\hat{ABD} = \hat{EBD}$ $(V ì B D l à t i a p h â n g i á c c ủ a \hat{ABC})$

Do đó: $ΔFDB = ΔCDB$ (G.C.G) BF = BC

Xét tam giác CKB và tam giác FKB có:

BK cạnh chung

BF = BC (cmt)

CK = KF (K là trung điểm của CF)

Do đó: $ΔCKB = ΔFKB$ (C.C.C)

=> $\hat{CBK} = \hat{FBK}$ => $B K l à t i a p h â n g i á c c ủ a \hat{ABC}$ (2)

Từ (1) và (2) => Ba điểm B;D;K thẳng hàng

Câu 2

Cho tam giác MNP có $\hat{N} = 90 °$ biết MN = 9cm; MP = 15cm độ dài cạnh PN là:

A. 12cm

B. 144 cm

C. 306 cm

\sqrt{306}

Lời giải

Vì tam giác MNP vuông tại N $(\hat{N} = 90 °)$ nên theo định lý Pytago ta có:

$N M^{2} + N P^{2} = M P^{2} \Rightarrow N P = \sqrt{M P^{2} - N M^{2}} = \sqrt{15^{2} - 9^{2}} = 12$ cm

Chọn đáp án A

Câu 3

Cho tam giác ABC vuông tại A biết $\hat{B} = 40 °$ khi đó:

A. BC > AC > AB

B. BC > AB > AC

C. AB > AC > BC

D. AC > AB > BC

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Cho đa thức A = x³ – 2x² + 3x + 2 – x³ + x – 2

a, Thu gọn đa thức A và tính giá trị của A tại $|x|$ = $\frac{1}{2}$

b, $T í n h t ổ n g M = A + B v à h i ệ u N = A - B b i ế t B = 3 x 2 - 2 x + 1 .$

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Bậc của đơn thức $- \frac{1}{2} x^{3} y z^{5}$ là:

A. 3

B. 5

C. 8

D. 9

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Đơn thức đồng dạng với đơn thức –5ab² là:

A. 2ab

B. 5a²b

C. 3b²a

D. a²b²

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 7

Cho bảng sau

Giá trị (x)

97

99

100

102

105

N = 40

Tần số (n)

3

5

29

2

1

A. 29

B. 99

C. 100

D. 103

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Toán

Văn

Vật lý

Hóa học

Lịch sử

Địa lý

Sinh học

Công nghệ

Giáo dục công dân

Tin học

Tiếng Anh

Giáo dục Kinh tế và Pháp luật

ĐHQG Hồ Chí Minh

ĐH Bách Khoa

ĐHQG Hà Nội

Bộ Công an

ĐHSP Hà Nội

Bằng lái xe

English Test

IT Test

Đại học

Toán

Văn

Vật lý

Hóa học

Lịch sử

Địa lý

Sinh học

Công nghệ

Tin học

Giáo dục Kinh tế và Pháp luật

Toán

Văn

Vật lý

Hóa học

Lịch sử

Địa lý

Sinh học

Công nghệ

Tin học

Giáo dục Kinh tế và Pháp luật

Toán

Văn

Vật lý

Hóa học

Lịch sử

Địa lý

Sinh học

Tin học

Giáo dục Kinh tế và Pháp luật

Global success

iLearn Smart World

Friends Global

Explore new worlds

Toán

Văn

Vật lý

Hóa học

Lịch sử

Địa lý

Sinh học

Công nghệ

Tin học

Giáo dục Quốc Phòng và An Ninh

Giáo dục Kinh tế và Pháp luật

Toán

Văn

Vật lý

Hóa học

Lịch sử

Địa lý

Sinh học

Công nghệ

Tin học

Giáo dục Quốc Phòng và An Ninh

Giáo dục Kinh tế và Pháp luật

Toán

Văn

Vật lý

Hóa học