Phương trình \[(x + 4)(x + 1) - 3\sqrt {{x^2} + 5x + 2} = 6\] có bao nhiêu nghiệm nguyên âm:
Phương trình \[(x + 4)(x + 1) - 3\sqrt {{x^2} + 5x + 2} = 6\] có bao nhiêu nghiệm nguyên âm:
A. 0;
B. 1;
C. 2;
D. 3;
Quảng cáo
Trả lời:
Đáp án đúng là: B
Điều kiện của phương trình: x2 + 5x + 2 ≥ 0\[ \Leftrightarrow \left[ \begin{array}{l}x \ge \frac{{ - 5 + \sqrt {17} }}{2}\\x \le \frac{{ - 5 - \sqrt {17} }}{2}\end{array} \right.\]
\[(x + 4)(x + 1) - 3\sqrt {{x^2} + 5x + 2} = 6 \Leftrightarrow {x^2} + 5x + 4 - 3\sqrt {{x^2} + 5x + 2} = 6\]
Đặt \[\sqrt {{x^2} + 5x + 2} = t(t \ge 0)\]
\[{x^2} + 5x + 4 - 3\sqrt {{x^2} + 5x + 2} = 6 \Leftrightarrow {t^2} - 3t - 4 = 0 \Leftrightarrow \left[ \begin{array}{l}t = - 1\\t = 4\end{array} \right.\]
Kết hợp với điều kiện t = 4 thỏa mãn
Với t = 4 ta có \[\sqrt {{x^2} + 5x + 2} = 4 \Leftrightarrow {x^2} + 5x - 14 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 2\\x = - 7\end{array} \right.\]
Vậy phương trình đã cho có 1 nghiệm nguyên âm.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Trọng tâm Toán, Văn, Anh 10 cho cả 3 bộ KNTT, CTST, CD VietJack - Sách 2025 ( 13.600₫ )
- Trọng tâm Lí, Hóa, Sinh 10 cho cả 3 bộ KNTT, CTST và CD VietJack - Sách 2025 ( 40.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
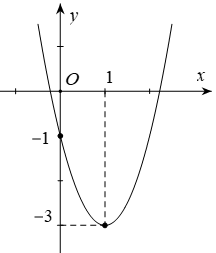
Câu 1
A. y = 2x2 – 4x – 1;
B. y = x2 – 2x – 1;
C. y = 2x2 – 8x – 1;
D. y = 2x2 – x – 1.
Lời giải
Đáp án đúng là: A
Dựa vào đồ thị ta có trục đối xứng x = 1
Đáp án A, B đều có trục đối xứng x = 1 nên A, B đều thỏa mãn
Đáp án C có trục đối xứng x = 2 nên loại đáp án C.
Đáp án D có trục đối xứng \[x = \frac{1}{4}\] nên loại đáp án D.
Dựa vào đồ thị ta có tọa độ đỉnh I(1; – 3)
Đáp án A có tọa độ đỉnh I(1; – 3) đáp án A thỏa mãn.
Đáp án B có tọa độ đỉnh I(1; – 2) nên loại đáp án B.
Câu 2
A. (– ∞; + ∞);
B. (– ∞; 1);
C. (1; + ∞);
D. (– ∞; 2).
Lời giải
Đáp án đúng là: B
Tọa độ đỉnh của hàm số là I(1; 2)
Bảng biến thiên
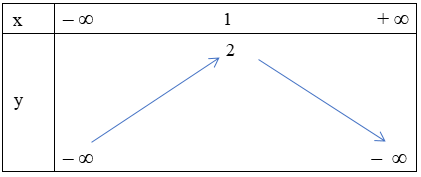
Từ bảng biến thiên ta có hàm số tăng từ trái sang phải trên khoảng (– ∞; 1) nên hàm số đồng biến trên khoảng (– ∞; 1).
Câu 3
A. Hàm số đồng biến trên (1; + ∞) ;
B. Đồ thị hàm số có trục đối xứng x = – 2;
C. Hàm số nghịch biến trên (– ∞; 1);
D. Đồ thị hàm số có đỉnh I(1; – 2).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. y = x2 + 2x + 1;
B. y = 5x2 – 2x + 1;
C. y = – x2 + 5x + 1;
D. y = 2x2 + x + 1.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. f(x) < 0 khi x ∈ (– 1; 1);
B. f(x) > 0 khi x ∈ (– ∞; –1) \( \cup \) (1; + ∞)
C. f(x) = 0 khi x = 1; x = – 1;
D. f(x) > 0 khi x ∈ (– 1; 1);
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. 1;
B. 0;
C. 2;
D. \[2\sqrt 2 \].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. m < 3;
B. m < 1;
C. m = 1;
D. 1 < m < 2.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.