Câu hỏi:

12/07/2024 4,913

Cho tam giác ABC vuông tại A, kẻ tia phân giác $\hat{A B C}$ cắt AC tại D.

a) Biết BC = 5cm, AB = 3 cm. Tính AC và AD.

b) Qua D kẻ DH vuông góc với BC tại H. Chứng minh ∆ABC ∆HDC từ đó chứng minh CH.CB = CD.CA.

c) E là hình chiếu của A trên BC. Chứng minh $\frac{B C}{B A} = \frac{H C}{H E}$ .
d) O là giao điểm của BD và AH. Qua B kẻ đường thẳng song song với AH cắt các tia CO và CA lần lượt tại M và N. Chứng minh M là trung điểm của BN.

Xem lời giải

Câu hỏi trong đề: Đề kiểm tra giữa kì 2 Toán 8 có đáp án ( Mới nhất) !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

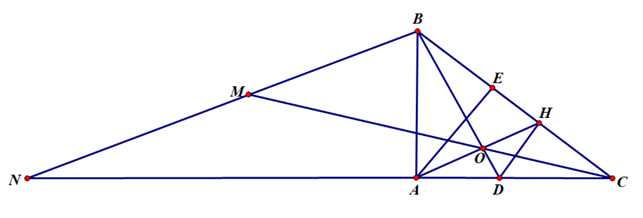
Cho tam giác ABC vuông tại A, kẻ tia phân giác gócABC cắt AC tại D a) Biết BC = 5cm, AB = 3cm, Tính AC và AD (ảnh 1)

a) Ta có ∆ABC vuông tại A nên ta có:

AB² + AC² = BC²( định lý Py – ta – go)

Þ AC² = BC² – AB² = 5² – 3² = 25 – 9 = 16

Þ AC = 4 (cm).

Xét ∆ABC có BD là tia phân giác của $\hat{A B C}$ (D Î AC)

Ta có: $\frac{A D}{D C} = \frac{B A}{B C}$ (định lý)

Mà DC = BC – AD = 5 – AD

$\Rightarrow \frac{A D}{5 - A D} = \frac{B A}{B C} = \frac{3}{5}$

Þ 5.AD = 3.(5 – AD)

Û 5AD = 15 – 3AD

Û 8AD = 15

Û AD = $\frac{15}{8}$ = 1,875 (cm)

Vậy độ dài đoạn AC là 4 cm và AD là 1,875 cm.

b) Theo đề ∆ABC vuông tại A nên có $\hat{B A C} = 90^{o}$ ;

DH vuông góc với BC tại H nên $\hat{D H C} = 90^{o}$ ;

Do đó $\hat{B A C} = \hat{D H C} = 90^{o}$ .

Xét ∆ABC và ∆HDC có:

$\hat{B C A}$ chung (giả thiết)

$\hat{B A C} = \hat{D H C} = 90^{o}$ (cmt)

Suy ra, ∆ABC $∽$ ∆HDC (g.g)

Vì ∆ABC $∽$ ∆HDC (cmt) nên $\frac{C H}{C A} = \frac{C D}{C B}$ (các cạnh tương ứng tỉ lệ)

Þ CH.CB = CA.CD.

c) Vì E là hình chiếu của A trên BC nên (E Î BC).

DH vuông góc với BC tại H (H Î BC).

Suy ra DH // AE (định lý)

Áp dụng định lý Ta – let trong ∆AEC có DH // AE (cmt)

Ta có: $\frac{H C}{H E} = \frac{D C}{D A}$ (1);

Xét ∆ABC có BD là tia phân giác của $\hat{A B C}$ (D Î AC)

Ta có: $\frac{B C}{B A} = \frac{D C}{D A}$ (2);

Từ (1) và (2) suy ra

\frac{H C}{H E} = \frac{B C}{B A} = \frac{D C}{D A}

Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

Bình luận

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Cho hai biểu thức $A = \frac{2 x}{x - 1}$ và $B = \frac{x}{x + 2} - \frac{x^{2} + 8}{x^{2} - 4} + \frac{3}{x - 2}$ với x ≠ 1; x ≠ ±2

a) Tính giá trị biểu thức A khi x = 3;

b) Rút gọn biểu thức B;
c) Tìm giá trị của x để A.B = 1.

Xem đáp án

Lời giải

a) Thay x = 3 (TMĐK) vào biểu thức $A = \frac{2 x}{x - 1}$ , ta được:

$A = \frac{2.3}{3 - 1} = \frac{2.3}{2} = 3;$

Vậy khi x = 3 thì giá trị biểu thức A = 3.

b) Với điều kiện x ≠ ±2, ta có:

$B = \frac{x}{x + 2} - \frac{x^{2} + 8}{x^{2} - 4} + \frac{3}{x - 2} = \frac{x (x - 2)}{(x + 2) (x - 2)} - \frac{x^{2} + 8}{x^{2} - 4} + \frac{3 (x + 2)}{(x - 2) (x + 2)} = \frac{x^{2} - 2 x}{(x + 2) (x - 2)} - \frac{x^{2} + 8}{(x + 2) (x - 2)} + \frac{3 x + 6}{(x + 2) (x - 2)} = \frac{x^{2} - 2 x - (x^{2} + 8) + 3 x + 6}{(x + 2) (x - 2)} = \frac{x^{2} - 2 x - x^{2} - 8 + 3 x + 6}{(x + 2) (x - 2)} = \frac{x - 2}{(x - 2) (x + 2)}$

= \frac{1}{x + 2}

(với x ≠ ±2)

c) Ta có: $A . B = \frac{2 x}{x - 1} . \frac{1}{x + 2} = \frac{2 x}{(x - 1) (x - 2)}$

Mà A.B = 1 nên $\frac{2 x}{(x - 1) (x - 2)} = 1$

Þ 2x = (x – 1)(x + 2) (vì x ≠ 1; x ≠ ±2)

Û 2x = x² + 2x – x – 2

Û 2x = x² + x – 2

Û x² + x – 2 – 2x = 0

Û x(x + 1) – 2 (1 + x) = 0

Û (x + 1)(x – 2) = 0

$\Leftrightarrow [\begin{matrix} x + 1 = 0 \\ x - 2 = 0 \end{matrix} \Leftrightarrow [\begin{matrix} x = - 1 \\ x = 2 \end{matrix}$

Đối chiếu với điều kiện x ≠ 1; x ≠ ±2, ta thấy chỉ có x = – 1 thỏa mãn.

Vậy để A.B = 1 thì x = – 1.

Câu 2

Cho phương trình $m = \frac{2 x + 1}{x - m}$ với m là tham số.
Tìm các số nguyên m để phương trình có nghiệm duy nhất với số tự nhiên.

Xem đáp án

Lời giải

Điều kiện xác định của phương trình $m = \frac{2 x + 1}{x - m}$ là:

x – m ≠ 0 suy ra x ≠ m.

Ta có: $m = \frac{2 x + 1}{x - m}$

$\Leftrightarrow \frac{m (x - m)}{x - m} = \frac{2 x + 1}{x - m} \Leftrightarrow \frac{m x - m^{2}}{x - m} = \frac{2 x + 1}{x - m}$

Þ mx – m² = 2x + 1

Û mx – 2x = m² + 1

Û x(m – 2) = m² + 1

$\Leftrightarrow x = \frac{m^{2} + 1}{m - 2} \Leftrightarrow x = m + 2 + \frac{5}{m - 2}$

Nghiệm của phương trình đã cho $x = m + 2 + \frac{5}{m - 2}$ với m – 2 ≠ 0 Û m ≠ 2

Để x Î N khi đó m – 2 Î Ư(5) = { ± 1; ± 5} và $m + 2 + \frac{5}{m - 2} \geq 0$

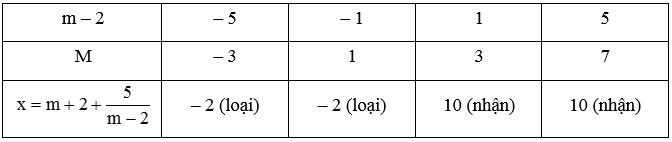
Cho phương trình m = 2x+1/x-m với m là tham số. tìm các số nguyên m để phương trình (ảnh 1)

Vậy m = {1;5} thì phương trình đã cho co nghiệm duy nhất x = 10.

Câu 3

Giải bài toán bằng cách lập phương trình:
Một người dự định đi ô tô từ A đến B với vận tốc 60 km/h. Nhưng thực tế người đó phải đến sớm hơn 30 phút để giải quyết công việc nên đã tăng tốc thêm 20 km/h so với dự định. Tính độ dài quãng đường từ A đến B.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Giải các phương trình sau:

a) 3(x – 1) – 7 = 5(x + 2);

b) $\frac{3 x + 1}{2} - \frac{x + 3}{5} = \frac{x}{10} + 2$ ;
c) $\frac{x - 2}{x + 1} - \frac{x}{x - 1} = \frac{x - 8}{x^{2} - 1}$ .

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Hỏi bài tập

Đăng ký gói thi VIP

VIP +1 tháng ( 199,000 VNĐ )

VIP +1 - Luyện thi tất cả các đề có trên Website trong 1 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +3 tháng ( 299,000 VNĐ )

VIP +3 - Luyện thi tất cả các đề có trên Website trong 3 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +6 tháng ( 399,000 VNĐ )

VIP +6 - Luyện thi tất cả các đề có trên Website trong 6 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +12 tháng ( 499,000 VNĐ )

VIP +12 - Luyện thi tất cả các đề có trên Website trong 12 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

Bình luận

Cho hai biểu thức A=2xx−1 và B=xx+2−x2+8x2−4+3x−2 với x ≠ 1; x ≠ ±2 a) Tính giá trị biểu thức A khi x = 3; b) Rút gọn biểu thức B; c) Tìm giá trị của x để A.B = 1.

Cho phương trình m=2x+1x−m với m là tham số. Tìm các số nguyên m để phương trình có nghiệm duy nhất với số tự nhiên.

Giải các phương trình sau: a) 3(x – 1) – 7 = 5(x + 2); b) 3x+12−x+35=x10+2 ; c) x−2x+1−xx−1=x−8x2−1 .

VIP +1 tháng ( 199,000 VNĐ )

VIP +3 tháng ( 299,000 VNĐ )

VIP +6 tháng ( 399,000 VNĐ )

VIP +12 tháng ( 499,000 VNĐ )

🔥 Đề thi HOT:

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đăng ký

Đăng nhập

Quên mật khẩu

Cho hai biểu thức $A = \frac{2 x}{x - 1}$ và $B = \frac{x}{x + 2} - \frac{x^{2} + 8}{x^{2} - 4} + \frac{3}{x - 2}$ với x ≠ 1; x ≠ ±2

a) Tính giá trị biểu thức A khi x = 3;

b) Rút gọn biểu thức B;
c) Tìm giá trị của x để A.B = 1.

Cho phương trình $m = \frac{2 x + 1}{x - m}$ với m là tham số.
Tìm các số nguyên m để phương trình có nghiệm duy nhất với số tự nhiên.

Giải các phương trình sau:

a) 3(x – 1) – 7 = 5(x + 2);

b) $\frac{3 x + 1}{2} - \frac{x + 3}{5} = \frac{x}{10} + 2$ ;
c) $\frac{x - 2}{x + 1} - \frac{x}{x - 1} = \frac{x - 8}{x^{2} - 1}$ .