Câu hỏi:
25/07/2022 488
Cho tam giác ABC cân tại A. Gọi M,N,H theo thứ tự là trung điểm của AB,AC và BC.
Kẻ , gọi K là trung điểm của EC. Qua K vẽ đường thẳng . Chứng minh: Ba đường thẳng AH, MN và d đồng qui (cùng gặp nhau tại 1 điểm)
Kẻ , gọi K là trung điểm của EC. Qua K vẽ đường thẳng . Chứng minh: Ba đường thẳng AH, MN và d đồng qui (cùng gặp nhau tại 1 điểm)
Câu hỏi trong đề: Bộ 14 đề thi Học kì 1 Toán 8 có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Phương pháp:
Lấy P là trung điểm cạnh ED. Gọi I là giao điểm của MN và AH. Ta sẽ chứng minh
Chỉ ra IAPK là hình bình hành, P là trực tâm tam giác ADK. Từ đó sử dụng quan hệ từ vuông góc đến song song để chứng minh .
Cách giải:
Kẻ , gọi K là trung điểm của EC. Qua K vẽ đường thẳng . Chứng minh: Ba đường thẳng AH, MN và d đồng qui (cùng gặp nhau tại 1 điểm)
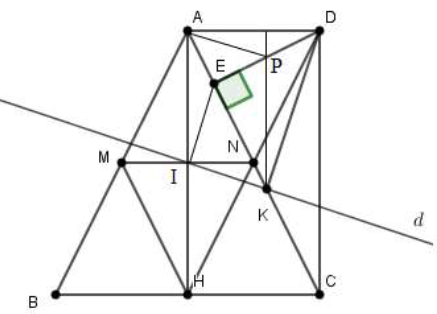
Lấy P là trung điểm cạnh ED. Gọi I là giao điểm của MN và AH. Ta sẽ chứng minh
Xét tam giác AHC có và N là trung điểm AC nên I là trung điểm của AH
Suy ra và ; (do ADCH là hình chữ nhật) nên
Xét tam giác EPC có PK là đường trung bình của tam giác ,
Xét tứ giác AIPK có ; nên AIPK là hình bình hành.
Do đó:
Lại có mà
Từ đó suy ra P là trực tâm tam giác ADK.
Suy ra mà nên
Do đó nên ba đường thẳng AH,MN, d đồng qui tại điểm I (đpcm).
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho tam giác ABC cân tại A. Gọi M,N,H theo thứ tự là trung điểm của AB,AC và BC.
Tứ giác BMNC và tứ giác BMNH là hình gì? Vì sao?
Cho tam giác ABC cân tại A. Gọi M,N,H theo thứ tự là trung điểm của AB,AC và BC.
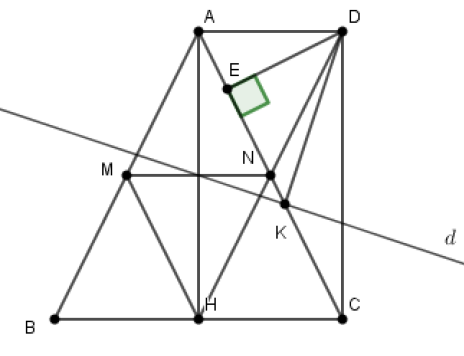
Tứ giác BMNC và tứ giác BMNH là hình gì? Vì sao?
Xem đáp án »
13/07/2024
1,155
Câu 2:
Một phòng học có kích thước dài 10m, rộng 6m. Người ta lát nền bằng gạch có hình vuông cạnh dài 50cm. Tính số tiền mua gạch để lát nền lớp học đó biết một thùng gạch giá 120000 đồng. (1 thùng có 8 viên gạch)
Một phòng học có kích thước dài 10m, rộng 6m. Người ta lát nền bằng gạch có hình vuông cạnh dài 50cm. Tính số tiền mua gạch để lát nền lớp học đó biết một thùng gạch giá 120000 đồng. (1 thùng có 8 viên gạch)
Xem đáp án »
11/07/2024
1,154
Câu 3:
Cho tam giác ABC cân tại A. Gọi M,N,H theo thứ tự là trung điểm của AB,AC và BC.
Gọi D là điểm đối xứng với H qua N. Chứng minh:ADCH là hình chữ nhật
Gọi D là điểm đối xứng với H qua N. Chứng minh:ADCH là hình chữ nhật
Xem đáp án »
11/07/2024
1,123
Câu 4:
Một tủ kệ trang trí hình tam giác đều có chu vi là 180cm, gồm 2 tam giác đều nhỏ và 1 hình thoi bên trong (như hình bên). Tính chu vi hình thoi?
Một tủ kệ trang trí hình tam giác đều có chu vi là 180cm, gồm 2 tam giác đều nhỏ và 1 hình thoi bên trong (như hình bên). Tính chu vi hình thoi?
Xem đáp án »
11/07/2024
726
Câu 5:
Bạn Việt muốn tính độ dài BC của một hồ bơi nhưng bạn chỉ đo được độ dài đoạn , biết M và N lần lượt là trung điểm của AC và AB. Bạn hãy tính độ dài BC dùm bạn Việt?
Bạn Việt muốn tính độ dài BC của một hồ bơi nhưng bạn chỉ đo được độ dài đoạn , biết M và N lần lượt là trung điểm của AC và AB. Bạn hãy tính độ dài BC dùm bạn Việt?
Xem đáp án »
25/07/2022
406
🔥 Đề thi HOT:
-
Bộ 10 đề thi cuối kì 2 Toán 8 Kết nối tri thức cấu trúc mới có đáp án (Đề 1)
-
15 câu Trắc nghiệm Toán 8 Kết nối tri thức Bài 1: Đơn thức có đáp án
-
Dạng 1: Bài luyện tập 1 dạng 1: Tính có đáp án
-
Đề kiểm tra cuối kỳ 2 Toán 8 có đáp án ( Mới nhất)_ đề 24
-
Bộ 10 đề thi giữa kì 2 Toán 8 Kết nối tri thức cấu trúc mới có đáp án (Đề 1)
-
Đề kiểm tra cuối kỳ 2 Toán 8 có đáp án ( Mới nhất)_ đề 1
-
Đề cuối kì 2 Toán 8 Chân trời sáng tạo cấu trúc mới có đáp án - Đề 1
-
Bộ 10 đề thi cuối kì 2 Toán 8 Kết nối tri thức cấu trúc mới có đáp án (Đề 2)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận