Cho hình chóp S.ABC có đường cao SA tam giác ABC là tam giác cân tại A có AB = a, . Biết thể tích khối chóp S.ABC bằng góc giữa hai mặt phẳng (SBC) và (ABC) bằng
A.
B.
C.
D.
Quảng cáo
Trả lời:
Phương pháp:
Xác định góc giữa các mặt phẳng (P) và (Q) ta thực hiện các bước sau:
+ Xác định giao tuyến d của (P) và (Q)
+ Trong mặt phẳng (P) xác định đường thẳng ad trong mặt phẳng (Q) xác định đường thẳng bd
+ Khi đó góc giữa (P) và (Q) là góc giữa hai đường thẳng a và b
Cách giải:

Gọi M là trung điểm BC => AMBC (do ABC cân tại A).
Lại có SAB = SAC(c.g.c) hay SBC cân tại S
=> SMBC
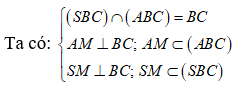
![]()
![]()

Theo đề bài
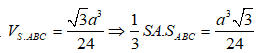

Lại thấy ABM vuông tại M có AB = a; ![]()
![]()
Xét tam giác SAM vuông tại A có SA = AM = nên SAM vuông cân tại A hay
Vậy góc giữa (SBC) và (ABC) bằng
Chọn D.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Chọn đáp án D.
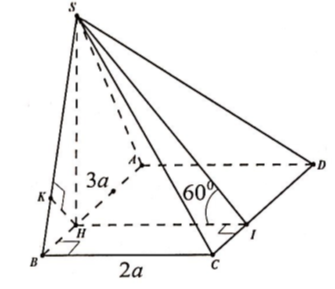
Ta có: ![]()
Kẻ 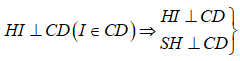
![]()
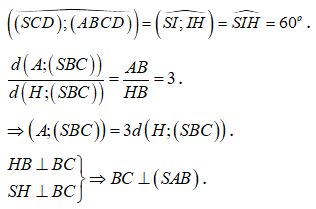
Kẻ ![]()
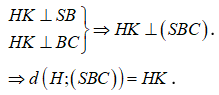
Xét tam giác SHI vuông tại H:
![]()
![]()
Xét tam giác SHB vuông tại B: 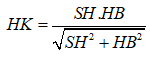
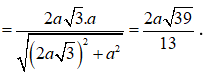
![]()
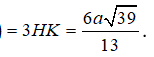
Lời giải
Chọn đáp án A
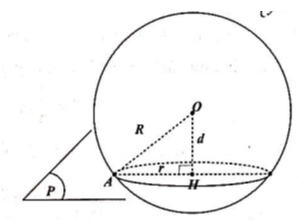
Bán kính hình cầu đã cho là
Khoảng cách từ tâm hình cầu đến mặt phẳng (P) là:
![]()
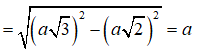
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. 20.
B. 30.
C. 10.
D. 60.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.