Cho $Δ A B C$ là tam giác nhọn, có AM là đường trung tuyến. Trên cạnh AC lấy hai điểm D và E sao cho $A D = D E = E C$ . AM cắt BD tại I.

Trên tia đối của tia CB lấy hai điểm P và Q sao cho $C P = P Q = C M$ . Chứng minh: ME, AP, DQ đồng quy tại một điểm.

Xem lời giải

Câu hỏi trong đề: Bộ 14 đề thi Học kì 1 Toán 8 có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Phương pháp:Chứng minh có một điểm đồng thời thuộc cả ba đường thẳng đó. hay F thuộc DQ.

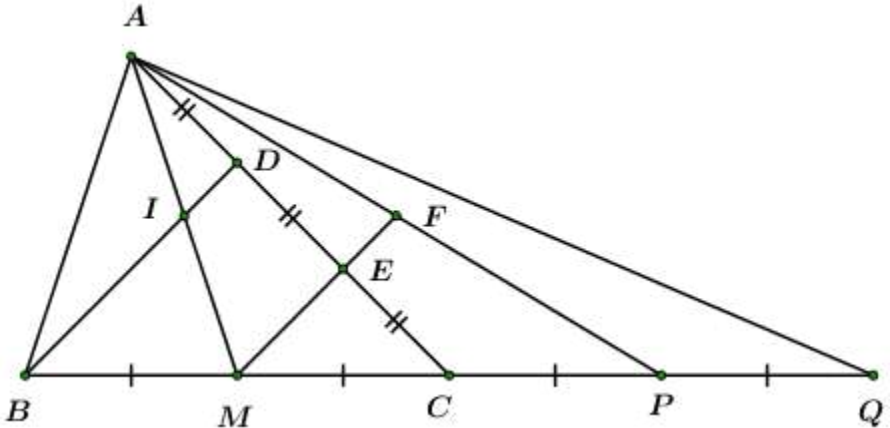
Cách giải:

Gọi $F = M E \cap A P$

Xét $Δ A M P$ có AC là đường trung tuyến, $A E = \frac{2}{3} A C$ Þ E là trọng tâm $Δ A M P$ $\Rightarrow E F = \frac{1}{2} M E$

$E F ∥ I D (d o M E ∥ I D : c m t); I D = E F = \frac{1}{2} M E$

Þ IDFE là hình bình hành (tứ giác có cặp cạnh đối song song và bằng nhau là hình bình hành)

$\Rightarrow I E ∥ D F (1)$

Ta có: $B I = \frac{3}{4} B D$ (chứng minh trên); $B P = \frac{3}{4} B Q$

$\Rightarrow I P ∥ D Q$ (định lý Ta-lét đảo trong tam giác)

IP là đường trung tuyến trong $Δ A M P$ $\Rightarrow I P \equiv I E \Rightarrow I E ∥ D Q (2)$

Từ (1) và (2) $\Rightarrow D F \equiv D Q$ hay $F \in D Q$

Vậy ME, DQ, AP đồng quy tại F.

Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Tìm giá trị nhỏ nhất của biểu thức sau: $A = 2 x^{2} + 10 y^{2} - 6 x y - 6 x - 2 y + 16$

Xem đáp án

Lời giải

Phương pháp:

Đưa biểu thức về dạng: $A = {[f (x)]}^{2} + a$

Khi đó biểu thức A min khi $f (x) = 0$ và GTNN của A chính bằng a.

Cách giải:

$A = 2 x^{2} + 10 y^{2} - 6 x y - 6 x - 2 y + 16$

$= x^{2} - 6 x y + 9 y^{2} + x^{2} - 6 x + 9 + y^{2} - 2 y + 1 + 6$

$= {(x - 3 y)}^{2} + {(x - 3)}^{2} + {(y - 1)}^{2} + 6$

Ta có: ${(x - 3 y)}^{2} \geq 0; {(x - 3)}^{2} \geq 0; {(y - 1)}^{2} \geq 0$ với mọi x, y

$A \min \Leftrightarrow \{\begin{cases} {(x - 3 y)}^{2} = 0 \\ {(x - 3)}^{2} = 0 \\ {(y - 1)}^{2} = 0 \end{cases} \Leftrightarrow \{\begin{cases} x - 3 y = 0 \\ x - 3 = 0 \\ y - 1 = 0 \end{cases} \Leftrightarrow \{\begin{cases} x = 3 y \\ x = 3 \\ y = 1 \end{cases} \Leftrightarrow \{\begin{cases} x = 3 \\ y = 1 \end{cases}$

Vậy GTNN của A là 6 khi $x = 3$ và $y = 1$ .

Câu 2

Phân tích các đa thức sau thành nhân tử: $x^{2} - 6 x y - 4 z^{2} + 9 y^{2}$

Xem đáp án

Lời giải

Phương pháp:

Phương pháp nhóm nhiều hạng tử kết hợp với dùng hằng đẳng thức.

Cách giải:

$(x^{2} - 6 x y - 4 z^{2} + 9 y^{2}) - 4 z^{2}$

$= [x^{2} - 2. x .3 y + {(3 y)}^{2}] - {(2 z)}^{2}$

$= {(x - 3 y)}^{2} - {(2 z)}^{2}$

$= (x - 3 y + 2 z) (x - 3 y - 2 z)$

Câu 3