Câu hỏi:

19/08/2025 768

Thực hiện phép chia đa thức: $(2 x^{4} + 11 x + 15 x^{2} - 13 x^{3} - 3)$ cho đa thức $(x^{2} - 4 x - 3)$ .

Tìm giá trị nhỏ nhất của đa thức thương trong phép chia đa thức trên.

Xem lời giải

Câu hỏi trong đề: Bộ 14 đề thi Học kì 1 Toán 8 có đáp án !!

Giao bài

Quảng cáo

Trả lời:

Giải bởi Vietjack

Phương pháp:

Biến đổi biểu thức, chia đa thức cho đa thức.

Sau đó biến đổi biểu thức thương tìm được về dạng: $A = {(f (x))}^{2} + c o n s t \geq c o n s t$ .

Dấu $" = "$ xảy ra $\Leftrightarrow f (x) = 0$ .

$\Rightarrow (2 x^{4} + 11 x + 15 x^{2} - 13 x^{3} - 3) : (x^{2} - 4 x - 3)$

Xét $A = 2 x^{2} - 5 x + 1$

$= 2 (x^{2} - \frac{5}{2} x + \frac{1}{2})$

$= 2 (x^{2} - 2. x . \frac{5}{4} + \frac{25}{16} - \frac{17}{16})$

$= 2 [{(x - \frac{5}{4})}^{2} - \frac{17}{16}]$

$= 2. {(x - \frac{5}{4})}^{2} - \frac{17}{8} \geq \frac{- 17}{8}$

Dấu $" = "$ xảy ra $\Leftrightarrow {(x - \frac{5}{4})}^{2} = 0 \Rightarrow x - \frac{5}{4} = 0 \Rightarrow x = \frac{5}{4}$

Vậy $M i n A = \frac{- 17}{8}$ khi $x = \frac{5}{4}$ .

Đang tải chế độ Học...

Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay

Các sản phẩm khác của Vietjack:

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Giữa hai điểm A và B là một hồ nước sâu. Biết lần lượt là trung điểm của (xem hình vẽ). Bạn Mai đi từ C đến D với vận tốc 160m/phút hết 1 phút 30 giây. Hỏi hai điểm A và B cách nhau bao nhiêu mét?

Xem đáp án

Lời giải

Phương pháp:

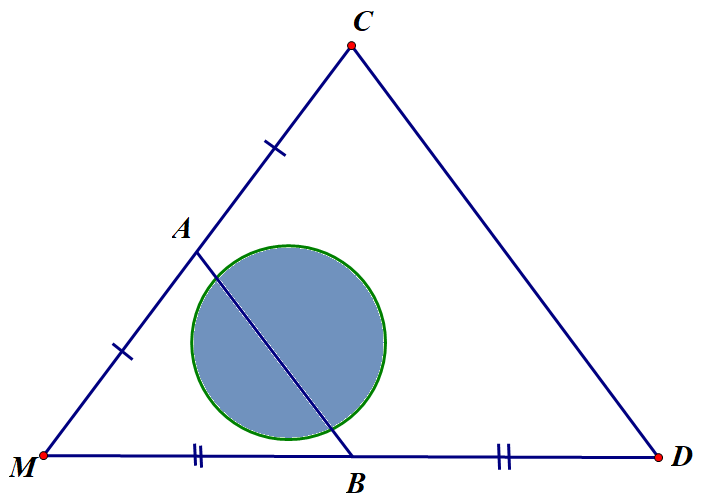
Dựa vào tính chất đường trung bình của tam giác.

Cách giải:

Đổi 1 phút 30 giây phút.

Xét $Δ M C D$ ta có:

A là trung điểm MC (gt)

B là trung điểm MD (gt)

$\Rightarrow A B$ là đường trung bình của (định lý).

$\Rightarrow A B = \frac{1}{2} C D$ (tính chất đường trung bình của tam giác).

Quãng đường bạn Mai đã đi là: $C D = 160.1,5 = 240 (m)$

$\Rightarrow A B = \frac{1}{2} .240 = 120 (m)$

Vậy hai điểm A và B cách nhau $120 m$ .

Câu 2

Phân tích đa thức thành nhân tử:

$9 x^{2} - 6 x + 1 - 16 y^{2}$

Xem đáp án

Lời giải

Phương pháp:

Phân tích đa thức thành nhân tử nhờ các phương pháp đặt nhân tử chung, nhóm hạng tử chung hoặc phương pháp hằng đẳng thức.

Cách giải:

$9 x^{2} - 6 x + 1 - 16 y^{2} = {(3 x - 1)}^{2} - 16 y^{2}$ $= (3 x - 1 - 4 y) (3 x - 1 + 4 y)$

Câu 3

Cho tam giác ABC vuông tại , D là trung điểm của cạnh BC. Vẽ DE vuông góc với AB tại E, DF vuông góc với AC tại F.

Trên tia đối của tia FD lấy điểm H sao cho . Chứng minh rằng tứ giác ADCH là hình thoi.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Cho tam giác ABC vuông tại , D là trung điểm của cạnh BC. Vẽ DE vuông góc với AB tại E, DF vuông góc với AC tại F.

Chứng minh rằng tứ giác AEDF là hình chữ nhật và $A D = E F$ .

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Cho tam giác ABC vuông tại , D là trung điểm của cạnh BC. Vẽ DE vuông góc với AB tại E, DF vuông góc với AC tại F.

Chứng minh rằng các đường thẳng $A D, B H, E F$ đồng quy.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Phân tích đa thức thành nhân tử:

$6 x^{3} - 6 x^{2}$

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.

Lớp 12

Lớp 11

Lớp 10

Ôn vào 10

Lớp 9

Lớp 8

Lớp 7

Lớp 6

Ôn vào 6

Lớp 5

Lớp 4

Lớp 3

Lớp 2

Lớp 1

Đại học

ĐGNL - ĐGTD

Tốt nghiệp THPT

Ôn vào 10

Ôn vào 6

V-ACT

HSA

TSA

SPT

Toán

Văn

Tiếng Anh

Vật lý

Hóa học

Sinh học

Lịch sử

Địa lý

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Văn

Tiếng Anh

Vật lí

Hóa học

Sinh học

Lịch sử

Địa lí

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Văn

Tiếng Anh

Vật lí

Hóa học

Sinh học

Lịch sử

Địa lí

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Văn

Tiếng Anh

Vật lý

Hóa học

Sinh học

Lịch sử

Địa lí

Giáo dục Kinh tế và Pháp luật

Tin học

Công nghệ

Toán

Văn

Tiếng Anh

Vật lý

Hóa học

Sinh học

Khoa học tự nhiên

Tin học

Lịch sử

Địa lí

Toán

Văn

Tiếng Anh

Thực hiện phép chia đa thức: $(2 x^{4} + 11 x + 15 x^{2} - 13 x^{3} - 3)$ cho đa thức $(x^{2} - 4 x - 3)$ .

Tìm giá trị nhỏ nhất của đa thức thương trong phép chia đa thức trên.

Phân tích đa thức thành nhân tử:

$9 x^{2} - 6 x + 1 - 16 y^{2}$

Cho tam giác ABC vuông tại , D là trung điểm của cạnh BC. Vẽ DE vuông góc với AB tại E, DF vuông góc với AC tại F.

Trên tia đối của tia FD lấy điểm H sao cho . Chứng minh rằng tứ giác ADCH là hình thoi.

Cho tam giác ABC vuông tại , D là trung điểm của cạnh BC. Vẽ DE vuông góc với AB tại E, DF vuông góc với AC tại F.

Chứng minh rằng tứ giác AEDF là hình chữ nhật và $A D = E F$ .

Cho tam giác ABC vuông tại , D là trung điểm của cạnh BC. Vẽ DE vuông góc với AB tại E, DF vuông góc với AC tại F.

Chứng minh rằng các đường thẳng $A D, B H, E F$ đồng quy.

Phân tích đa thức thành nhân tử:

$6 x^{3} - 6 x^{2}$