Câu hỏi:

27/07/2022 900

Cho tam giác ABC vuông tại , D là trung điểm của cạnh BC. Vẽ DE vuông góc với AB tại E, DF vuông góc với AC tại F.

Chứng minh rằng các đường thẳng $A D, B H, E F$ đồng quy.

Xem lời giải

Câu hỏi trong đề: Bộ 14 đề thi Học kì 1 Toán 8 có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Phương pháp:

Sử dụng tính chất hình bình hành.

Cách giải:

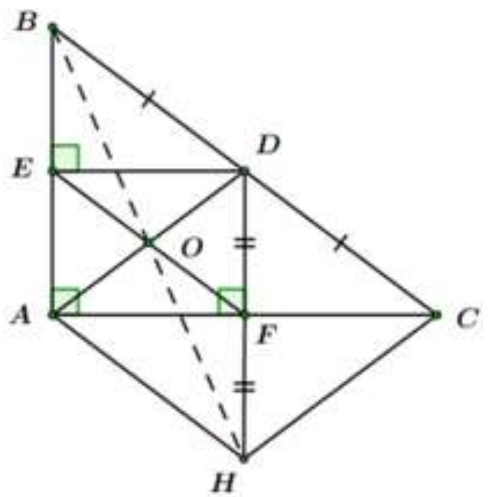
Chứng minh rằng các đường thẳng AD, BH, EF đồng quy.

Gọi O là giao điểm của AD và EF.

$\Rightarrow O$ là trung điểm của AD và EF.

Ta có tứ giác ADCH là hình thoi (cmt)

$\Rightarrow \{\begin{cases} D C // A H \\ D C = A H \end{cases}$ (tính chất hình thoi).

Mà $B D = D C (g t) \Rightarrow B D = A H (= D C)$ .

Xét tứ giác ABDH ta có:

$A H // B D (A H // D C)$

$A H = B D$ (cmt)

$\Rightarrow A B D H$ là hình bình hành. (dhnb)

$\Rightarrow A D$ cắt BH tại trung điểm của mỗi đường. (tính chất hbh).

Mà O là trung điểm của $A D \Rightarrow O \in B H$ .

$\Rightarrow A D, E F, B H$ đồng quy tại O.

Media VietJack

Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Giữa hai điểm A và B là một hồ nước sâu. Biết lần lượt là trung điểm của (xem hình vẽ). Bạn Mai đi từ C đến D với vận tốc 160m/phút hết 1 phút 30 giây. Hỏi hai điểm A và B cách nhau bao nhiêu mét?

Xem đáp án

Lời giải

Phương pháp:

Dựa vào tính chất đường trung bình của tam giác.

Cách giải:

Đổi 1 phút 30 giây phút.

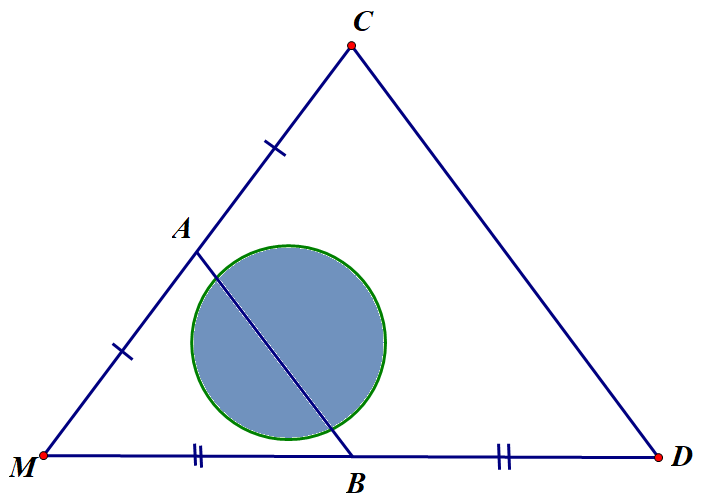
Xét $Δ M C D$ ta có:

A là trung điểm MC (gt)

B là trung điểm MD (gt)

$\Rightarrow A B$ là đường trung bình của (định lý).

$\Rightarrow A B = \frac{1}{2} C D$ (tính chất đường trung bình của tam giác).

Quãng đường bạn Mai đã đi là: $C D = 160.1,5 = 240 (m)$

$\Rightarrow A B = \frac{1}{2} .240 = 120 (m)$

Vậy hai điểm A và B cách nhau $120 m$ .

Câu 2

Phân tích đa thức thành nhân tử:

$9 x^{2} - 6 x + 1 - 16 y^{2}$

Xem đáp án

Lời giải

Phương pháp:

Phân tích đa thức thành nhân tử nhờ các phương pháp đặt nhân tử chung, nhóm hạng tử chung hoặc phương pháp hằng đẳng thức.

Cách giải:

$9 x^{2} - 6 x + 1 - 16 y^{2} = {(3 x - 1)}^{2} - 16 y^{2}$ $= (3 x - 1 - 4 y) (3 x - 1 + 4 y)$

Câu 3

Cho tam giác ABC vuông tại , D là trung điểm của cạnh BC. Vẽ DE vuông góc với AB tại E, DF vuông góc với AC tại F.

Trên tia đối của tia FD lấy điểm H sao cho . Chứng minh rằng tứ giác ADCH là hình thoi.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Cho tam giác ABC vuông tại , D là trung điểm của cạnh BC. Vẽ DE vuông góc với AB tại E, DF vuông góc với AC tại F.

Chứng minh rằng tứ giác AEDF là hình chữ nhật và $A D = E F$ .

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Thực hiện phép chia đa thức: $(2 x^{4} + 11 x + 15 x^{2} - 13 x^{3} - 3)$ cho đa thức $(x^{2} - 4 x - 3)$ .

Tìm giá trị nhỏ nhất của đa thức thương trong phép chia đa thức trên.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Phân tích đa thức thành nhân tử:

$6 x^{3} - 6 x^{2}$

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Cho tam giác ABC vuông tại , D là trung điểm của cạnh BC. Vẽ DE vuông góc với AB tại E, DF vuông góc với AC tại F. Chứng minh rằng các đường thẳng AD,BH,EF đồng quy.

Giữa hai điểm A và B là một hồ nước sâu. Biết lần lượt là trung điểm của (xem hình vẽ). Bạn Mai đi từ C đến D với vận tốc 160m/phút hết 1 phút 30 giây. Hỏi hai điểm A và B cách nhau bao nhiêu mét?

Phân tích đa thức thành nhân tử: 9x2−6x+1−16y2

Cho tam giác ABC vuông tại , D là trung điểm của cạnh BC. Vẽ DE vuông góc với AB tại E, DF vuông góc với AC tại F. Trên tia đối của tia FD lấy điểm H sao cho . Chứng minh rằng tứ giác ADCH là hình thoi.

Cho tam giác ABC vuông tại , D là trung điểm của cạnh BC. Vẽ DE vuông góc với AB tại E, DF vuông góc với AC tại F. Chứng minh rằng tứ giác AEDF là hình chữ nhật và AD=EF .

Thực hiện phép chia đa thức: 2x4+11x+15x2−13x3−3 cho đa thức x2−4x−3 . Tìm giá trị nhỏ nhất của đa thức thương trong phép chia đa thức trên.

Phân tích đa thức thành nhân tử: 6x3−6x2

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đăng ký

Đăng nhập

Quên mật khẩu

Cho tam giác ABC vuông tại , D là trung điểm của cạnh BC. Vẽ DE vuông góc với AB tại E, DF vuông góc với AC tại F.

Chứng minh rằng các đường thẳng $A D, B H, E F$ đồng quy.

Phân tích đa thức thành nhân tử:

$9 x^{2} - 6 x + 1 - 16 y^{2}$

Cho tam giác ABC vuông tại , D là trung điểm của cạnh BC. Vẽ DE vuông góc với AB tại E, DF vuông góc với AC tại F.

Trên tia đối của tia FD lấy điểm H sao cho . Chứng minh rằng tứ giác ADCH là hình thoi.

Cho tam giác ABC vuông tại , D là trung điểm của cạnh BC. Vẽ DE vuông góc với AB tại E, DF vuông góc với AC tại F.

Chứng minh rằng tứ giác AEDF là hình chữ nhật và $A D = E F$ .

Thực hiện phép chia đa thức: $(2 x^{4} + 11 x + 15 x^{2} - 13 x^{3} - 3)$ cho đa thức $(x^{2} - 4 x - 3)$ .

Tìm giá trị nhỏ nhất của đa thức thương trong phép chia đa thức trên.

Phân tích đa thức thành nhân tử:

$6 x^{3} - 6 x^{2}$