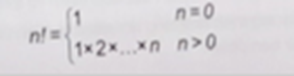Giải SBT Tin 9 KNTT Bài 15. Bài toán tin học có đáp án
37 người thi tuần này 4.6 431 lượt thi 11 câu hỏi
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề thi cuối kì 2 Tin học 9 Kết nối tri thức có đáp án - Đề 3
Đề thi cuối kì 2 Tin học 9 Kết nối tri thức có đáp án - Đề 2
Đề thi cuối kì 2 Tin học 9 Kết nối tri thức có đáp án - Đề 1
Đề thi cuối kì 2 Tin học 9 Chân trời sáng tạo có đáp án - Đề 3
Đề thi cuối kì 2 Tin học 9 Chân trời sáng tạo có đáp án - Đề 2
Đề thi cuối kì 2 Tin học 9 Chân trời sáng tạo có đáp án - Đề 1
Đề thi cuối kì 2 Tin học 9 Cánh Diều có đáp án - Đề 3
Đề thi cuối kì 2 Tin học 9 Cánh Diều có đáp án - Đề 2
Danh sách câu hỏi:
Lời giải
a) Đầu vào: ba số nguyên dương.
Đầu ra: Các cụm từ "Không là tam giác", "Tam giác thường", "Tam giác cân", "Tam giác đều", "Tam giác vuông", "Tam giác vuông cân" tuỳ theo độ dài ba cạnh đầu vào.
b) Chúng ta sử dụng một số quy tắc lặp để thực hiện các bước như sau:
Các cấu trúc cơ bản trong Scratch:
Các chỉ dẫn (câu lệnh) cùng tham vi tác động của một câu trúc lặp hay rẽ nhánh sẽ được viết lùi lại, cùng mức căn lề trái. Các chỉ dẫn (câu lệnh) không cùng tham vi tác động với các thẻ dòng liên tiếp (cùng mức căn lề trái) nhưng có thẻ dòng rẽ nhánh các cấp lùi bằng dấu {}.
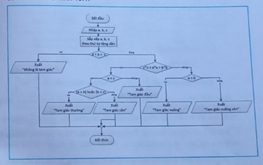
Thuật toán phân loại tam giác theo ba cạnh đầu vào được mô tả cách liệt kê các bước như sau:
Nhập ba số a, b, c.
Nếu (a > b) thì hoán đổi giá trị a và b
Nếu (b > c) thì hoán đổi giá trị b và c
Nếu (a > b) thì hoán đổi giá trị a và b
Nếu (a + b > c) thì
Nếu (c*c = b*b + a*a) thì
Nếu (a = b) thì xuất "Tam giác vuông cân"
còn không thì xuất "Tam giác vuông"
còn không thì
Nếu (a = c) thì xuất "Tam giác đều"
còn không thì
Nếu (a = b) hoặc (b = c) thì xuất "Tam giác cân"
còn không thì xuất "Tam giác thường"
còn không thì xuất "Không là tam giác"
Việc sắp xếp ba giá trị đầu vào theo thứ tự (chẳng hạn tăng dần) sẽ giúp việc kiểm tra điều kiện trở nên đơn giản hơn. Thuật toán cũng có thể mô tả bằng sơ đồ khối như Hình 15.1.
Lời giải
Gọi ước chung lớn nhất của hai số a và b là UCLN(a, b). Thuật toán này đã được đề cập đến trong bài tập Vận dụng 2, Bài 14 (trang 85 Tin học 8). Khi đó phân số a/b sẽ được rút gọn bằng cách chia cả tử số và mẫu số cho UCLN(a, b). Lưu ý rằng, khi UCLN(a, b) giữ cố định để thay đổi nên tử số và mẫu số của phân số luôn luôn biến khác, chẳng hạn vào hai biến c và d như trong Hình 15.2a.
Lời giải
Đầu vào: số nguyên dương nnn.
Đầu ra: số Fibonacci thứ nnn và tổng của n số Fibonacci đầu tiên.
Ví dụ:
|
Đầu vào |
Đầu ra |
Giải thích |
|
3 |
2, 4 |
Những số Fibonacci đầu tiên là 0, 1, 1, 2, 3,... |
|
5 |
5, 12 |
Những số Fibonacci đầu tiên là 0, 1, 1, 2, 3,... |
b) Thuật toán tính số Fibonacci thứ n và tổng n số Fibonacci đầu tiên có thể được mô tả theo các bước như sau:
Nhập n
Nếu n = 1 thì
f ß 0; s ß0
còn không thì
Nếu n = 2 thì
f ß 1; s ß 1
còn không thì
aß 0; b ß 1; s ß 1
Lặp (n-2) bước
f ß a + b; s ß s + f; a ß b; b ß f;
Xuất f, s
Lời giải
Đầu vào: số nguyên dương n.
Đầu ra: tổng s=13+23…+n3
Thuật toán tính tổng lập phương của n số tự nhiên đầu tiên được trình bày theo các bước như sau:
Nhập n
i ß 0; s ß 0
Lặp n bước
i ß i + 1; s ß s + i * i * i;
Xuất s
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.