Bài tập cuối chương 6

Lời giải:

Để sắp xếp các số thập phân sau theo thứ tự giảm dần, ta làm như sau:

Bước 1: Chia thành 2 nhóm số thập phân dương và số thập phân âm, vì số thập phân dương luôn lớn hơn số thập phân âm.

Bước 2: Ta so sánh các số thập phân theo nhóm với nhau:

- Nhóm các số thập phân dương: ta so sánh phần nguyên với nhau, số nào có phần nguyên lớn hơn thì lớn hơn. Nếu phần nguyên bằng nhau thì ta lần lượt so sánh các hàng ở phần thập phân.

- Nhóm các số thập phân âm: ta so sánh số đối của chúng, số nào có số đối lớn hơn thì nhỏ hơn.

Đối với bài toán này, ta thực hiện theo thứ tự các bước như trên:

* Phân loại:

- Nhóm các số thập phân dương: 0,6; 1,41; 5,4; 0,22.

- Nhóm các số thập phân âm: −5,24; −4,125; −0,26.

* So sánh các số thập phân trong theo nhóm:

- Nhóm các số thập phân dương:

+ Phần nguyên của số 0,6 và 0,22 là 0; ta so sánh hàng phần mười của hai số. Vì 6 > 2 nên 0,6 > 0,22.

+ Phần nguyên của số 1,41 là 1;

+ Phần nguyên của số 5,4 là 5.

Do đó 5,4 > 1,41 > 0,6 > 0,22 (các số có phần nguyên lớn hơn thì số đó lớn hơn).

- Nhóm các số thập phân âm:

+ Số đối của các số −5,24; −4,125; −0,26 lần lượt là 5,24; 4,125; 0,26.

+ Chữ số hàng phần mười của các số 5,24; 4,125; 0,26 lần lượt là 5; 4; 0.

+ Ta so sánh phần nguyên của các số trên:

Vì 0 < 4 < 5 nên 0,26 < 4,125 < 5,24. Suy ra −0,26 > −4,125 > −5,24.

Do đó 5,4 > 1,41 > 0,6 > 0,22 > −0,26 > −4,125 > −5,24.

Vậy các số được sắp xếp thứ tự giảm dần là: 12,79; 5,17; 0,6; 0,22; −0,26; −4,125; −5,24.

Lời giải:

Để sắp xếp các số thập phân sau theo thứ tự tăng dần, ta làm như sau:

Bước 1: Chia thành 2 nhóm số thập dương và số thập phân âm, vì số thập phân âm luôn nhỏ hơn số thập phân dương.

Bước 2: Ta so sánh các số thập phân theo nhóm với nhau:

- Nhóm các số thập phân dương: ta so sánh phần nguyên với nhau, số nào có phần nguyên lớn hơn thì lớn hơn. Nếu phần nguyên bằng nhau thì ta lần lượt so sánh các hàng ở phần thập phân.

- Nhóm các số thập phân âm: ta so sánh số đối của chúng, số nào có số đối lớn hơn thì nhỏ hơn.

Đối với bài toán này, ta thực hiện theo thứ tự các bước như trên:

* Phân loại:

- Nhóm các số thập phân dương: 0,124; 0,12.

- Nhóm các số thập phân âm: −4,23; −0,12; −0,02; −0,001; −1,28.

* So sánh các số thập phân trong theo nhóm:

- Nhóm các số thập phân dương:

+ Hai số 0,124; 0,12 có cùng phần nguyên nên ta so sánh phần thập phân.

+ Hàng phần mười và hàng phần trăm của hai số này đều bằng nhau.

+ Ta so sánh hàng phần nghìn của hai số, hàng phần nghìn của 0,124 và 0,12 lần lượt là 4 và 0. Vì 4 > 0 nên 0,124 > 0,12.

- Nhóm các số thập phân âm:

+ Số đối của các số −4,23; −0,12; −0,02; −0,001; −1,28 lần lượt là 4,23; 0,12; 0,02; 0,001; 1,28.

+ Số 4,23 có phần nguyên là 4;

+ Số 1,28 có phần nguyên là 1;

+ Các số 0,12; 0,02; 0,001 đều có phần nguyên là 0 nên ta so sánh phần thập phân của các số

+) Số 0,12 có hàng phần mười là 1.

+) Các số 0,02; 0,001 đều có hàng phần mười là 0, ta tiếp tục so sánh hàng phần trăm của hai số, hàng phần trăm của 0,02; 0,001 lần lượt là 2 và 0. Vì 2 > 0 nên 0,02 > 0,001.

Do đó 4,23 > 1,28 > 0,02 > 0,001 hay −4,23 < −1,28 < −0,02 < −0,001.

Vậy các số được sắp xếp thứ tự tăng dần là: −4,23; −1,28; −0,02; −0,001; 0,12; 0,124.

Lời giải:

Mức lương tối thiểu vùng I năm 2018 tăng so với năm 2017 là:

3 980 000 − 3 750 000 = 230 000 (đồng)

Phần trăm lương tối thiểu vùng I năm 2018 tăng so với năm 2017 là:

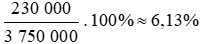
Vậy phần trăm lương tối thiểu vùng I năm 2018 tăng so với năm 2017 là khoảng 6,13%.

Lời giải:

Lượng điện năng tiêu thụ của tháng 3/2019 tăng so với tháng 2/2019 là:

2,38 − 1,65 = 0,73 (tỉ kWh)

Phần trăm lượng điện năng tiêu thụ tháng 3/2019 tăng so với tháng 2/2019 là:

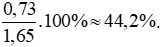
Vậy phần trăm lượng điện năng tiêu thụ tháng 3/2019 tăng so với tháng 2/2019 là 44,2%.

Lời giải:

Nếu không tính tiền phục vụ thì phần trăm số tiền người đó trả cho bữa ăn so với số tiền đã trả là:

100% − 10% = 90%.

Nếu không tính tiền phục vụ thì số tiền thực mà khách cần trả là:

2 750 000 . 90% = 2 475 000 (đồng).

Vậy nếu không tính tiền phục vụ thì số tiền thực mà khách cần trả cho bữa ăn là 2 475 000 đồng.