Cho góc nhọn xOy và một điểm A nằm trong góc đó. Kẻ AH \(\bot\) Ox tại H và AK \(\bot\) Oy tại K. Kéo dài AH một đoạn HB = AH và kéo dài AK một đoạn KC = AK. Nối OA, OB, OC. Chọn phát biểu đúng:
Cho góc nhọn xOy và một điểm A nằm trong góc đó. Kẻ AH \(\bot\) Ox tại H và AK \(\bot\) Oy tại K. Kéo dài AH một đoạn HB = AH và kéo dài AK một đoạn KC = AK. Nối OA, OB, OC. Chọn phát biểu đúng:
A. OA = OB = OC;
B. \(\widehat {HOK} = \frac{1}{2}\widehat {BOC};\)
C. Cả A và B đều đúng;
D. Cả A và B đều sai.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án đúng là: C
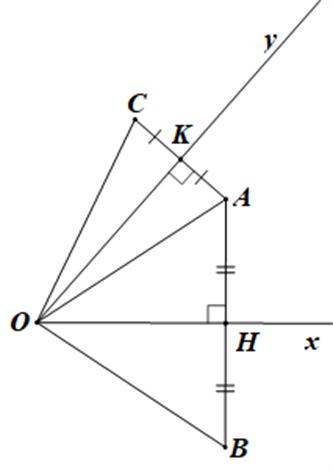
Xét tam giác OAH và tam giác OBH có:
OH là cạnh chung,
\(\widehat {OHA} = \widehat {OHB}\left( { = 90^\circ } \right),\)
AH = BH (giả thiết)
Do đó \(\Delta\)OAH = \(\Delta\)OBH (c.g.c)
Suy ra OA = OB (hai cạnh tương ứng) (1)
Chứng minh tương tự ta cũng có \(\Delta\)OKA = \(\Delta\)OKC (c.g.c)
Suy ra OA = OC (hai cạnh tương ứng) (2)
Từ (1) và (2) suy ra OA = OB = OC. Do đó A là khẳng định đúng.
Vì \(\Delta\)OAH = \(\Delta\)OBH (c.g.c) (chứng minh trên)
Nên \(\widehat {AOH} = \widehat {BOH}\) (hai góc tương ứng)
Suy ra OH là tia phân giác của \(\widehat {AOB}\)
Do đó \(\widehat {AOH} = \widehat {BOH} = \frac{1}{2}\widehat {AOB}\) (3)
Tương tự ta cũng có OK là tia phân giác của \(\widehat {COA}\)
Do đó \(\widehat {KOA} = \widehat {COK} = \frac{1}{2}\widehat {COA}\) (4)
Từ (3) và (4) ta có: \(\widehat {KOA} + \widehat {AOH} = \frac{1}{2}\widehat {COA} + \frac{1}{2}\widehat {AOB}\)
Hay \(\widehat {HOK} = \frac{1}{2}\left( {\widehat {COA} + \widehat {AOB}} \right) = \frac{1}{2}\widehat {COB}\). Do đó B là khẳng định đúng
Vậy ta chọn phương án C.
Hot: 1000+ Đề thi cuối kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. Chỉ có (1) đúng;
B. Chỉ có (2) đúng;
C. Cả (1) và (2) đều đúng;
D. Cả (1) và (2) đều sai.
Lời giải
Đáp án đúng là: C
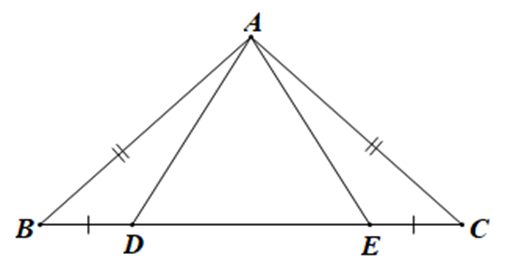
+ Xét \(\Delta\)ABD và \(\Delta\)ACE có:
AB = AC (giả thiết),
\(\widehat {ABD} = \widehat {ACE}\) (giả thiết),
BD = CE (giả thiết)
Do đó \(\Delta\)ABD = \(\Delta\)ACE (c.g.c)
+ Vì BE = BD + DE, CD = CE + ED
Mà BD = CE (giả thiết) nên BE = CD.
Xét \(\Delta\)ABE và \(\Delta\)ACD có:
AB = AC (giả thiết),
\(\widehat {ABE} = \widehat {ACD}\) (giả thiết),
BE = CD (chứng minh trên)
Do đó \(\Delta\)ABE = \(\Delta\)ACD (c.g.c)
Vậy cả phương án A và B đều đúng, ta chọn phương án C.
Câu 2
A. 60°;
B. 90°;
C. 100°;
D. 120°.
Lời giải
Đáp án đúng là: B
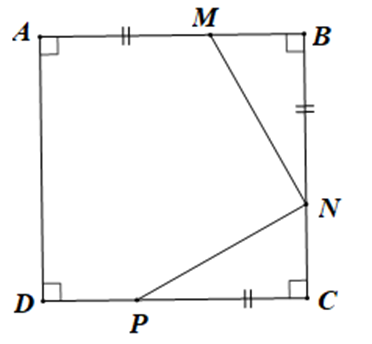
Vì ABCD là hình vuông (giả thiết) nên AB = BC (tính chất hình vuông)
Do đó AM + MB = BN + NC
Mà AM = BN (giả thiết) nên MB = NC.
Xét tam giác MBN và tam giác NCP có:
BN = CP (giả thiết),
\(\widehat B = \widehat C\) (\( = 90^\circ ,\) tính chất hình vuông),
MB = NC (chứng minh trên)
Do đó \(\Delta\)MBN = \(\Delta\)NCP (c.g.c)
Suy ra \(\widehat {BMN} = \widehat {CNP}\) (hai góc tương ứng)
Mà \(\widehat {BMN} + \widehat {BNM} = 90^\circ \) (trong tam giác BMN vuông tại B, hai góc nhọn phụ nhau)
Do đó \(\widehat {BNM} + \widehat {CNP} = 90^\circ \)
Mặt khác \(\widehat {BNM} + \widehat {MNP} + \widehat {CNP} = 180^\circ \)
Suy ra \(\widehat {MNP} = 180^\circ - \left( {\widehat {BNM} + \widehat {CNP}} \right) = 180^\circ - 90^\circ = 90^\circ \)
Vậy \(\widehat {MNP} = 90^\circ .\)
Câu 3
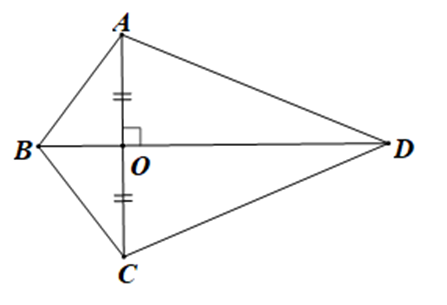
A. \(\widehat {AOC} = \widehat {BOC};\)
B. CA = CB;
C. CO là tia phân giác của \(\widehat {ACB};\)
D. Cả A, B, C đểu đúng.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
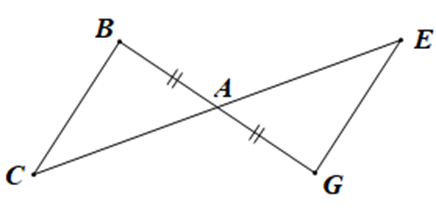
A. AC = DG;
B. BC = EG;
C. \(\widehat {ACB} = \widehat {DGE};\)
D. Tất cả đều sai.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. CE \(\bot\) AB;
B. BD \(\bot\) CE;
C. BD \(\bot\) AC;
D. \(\widehat {CBD} = \widehat {BCE}.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. 1;
B. 2;
C. 3;
D. 4.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. \(\widehat {ACB} = \widehat {AGE};\)
B. AC = EG;
C. AC = AE;
D. BC = AG.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập