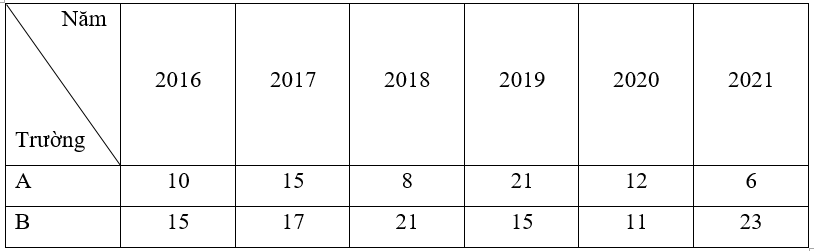
Số lượng bệnh nhân khỏi bệnh của hai bệnh viện A và B trong 6 ngày được thống kê trong bảng dưới đây:
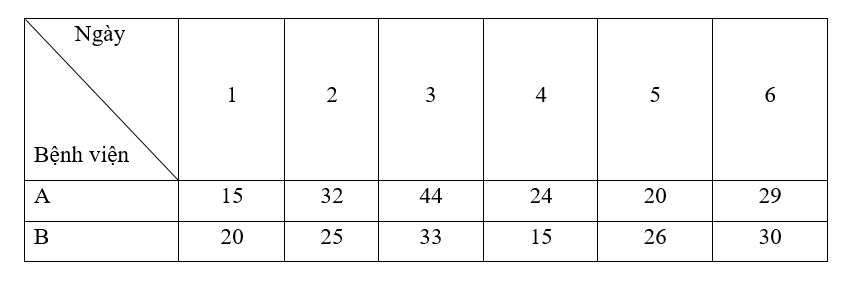
Sử dụng kiến thức về khoảng biến thiên và khoảng tứ phân vị, xác định xem số lượng bệnh nhân khỏi bệnh của bệnh viện nào ổn định hơn?
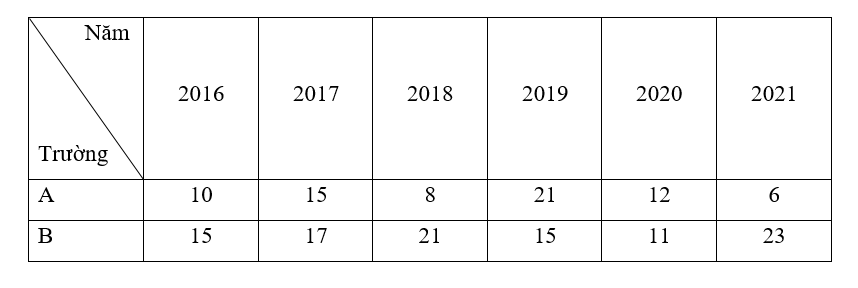
Số lượng bệnh nhân khỏi bệnh của hai bệnh viện A và B trong 6 ngày được thống kê trong bảng dưới đây:

Sử dụng kiến thức về khoảng biến thiên và khoảng tứ phân vị, xác định xem số lượng bệnh nhân khỏi bệnh của bệnh viện nào ổn định hơn?
Quảng cáo
Trả lời:
Hướng dẫn giải:
Đáp án đúng là: B.
- Sắp xếp số lượng bệnh nhân khỏi bệnh của bệnh viện A theo thứ tự không giảm ta có:
15; 20; 24; 29; 32; 44.
+ Giá trị nhỏ nhất của mẫu số liệu trên là 15
+ Giá trị lớn nhất của mẫu số liệu trên là 44
Suy ra khoảng biến thiên RA = 44 – 15 = 29.
Ta lại có:
+ Giá trị tứ phân vị thứ nhất là trung vị của mẫu: 15; 20; 24.
Do đó Q1A = 20.
+ Giá trị tứ phân vị thứ ba là trung vị của mẫu: 29; 32; 44.
Do đó Q3A = 32.
Suy ra khoảng tứ phân vị ∆QA = Q3A – Q1A = 32 – 20 = 12.
- Sắp xếp số lượng bệnh nhân khỏi bệnh của bệnh viện B theo thứ tự không giảm ta có:
15; 20; 25; 26; 30; 33.
+ Giá trị nhỏ nhất của mẫu số liệu trên là 15
+ Giá trị lớn nhất của mẫu số liệu trên là 33
Suy ra khoảng biến thiên RB = 33 – 15 = 18.
Ta lại có:
+ Giá trị tứ phân vị thứ nhất là trung vị của mẫu: 15; 20; 25.
Do đó Q1B = 20.
+ Giá trị tứ phân vị thứ ba là trung vị của mẫu: 26; 30; 33.
Do đó Q3B = 30.
Suy ra ∆QB = Q3B – Q1B = 30 – 20 = 10.
Do đó khoảng tứ phân vị của mẫu số liệu trên là 10.
Ta thấy khoảng biến thiên và khoảng tứ phân vị trong số lượng bệnh nhân khỏi bệnh của bệnh viện B bé hơn bệnh viện A nên số lượng bệnh nhân khỏi bệnh của bệnh viện B ổn định hơn.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Sách - Sổ tay kiến thức trọng tâm Vật lí 10 VietJack - Sách 2025 theo chương trình mới cho 2k9 ( 31.000₫ )
- Trọng tâm Lí, Hóa, Sinh 10 cho cả 3 bộ KNTT, CTST và CD VietJack - Sách 2025 ( 40.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
Hướng dẫn giải:
Đáp án đúng là: B.
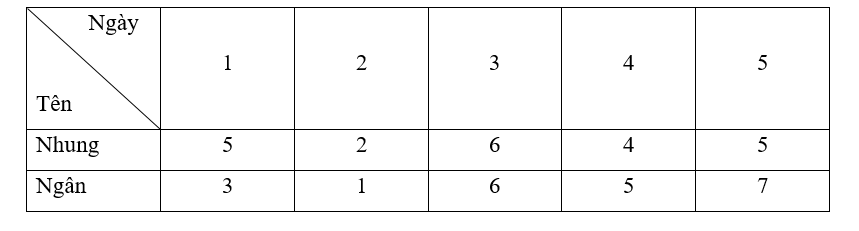
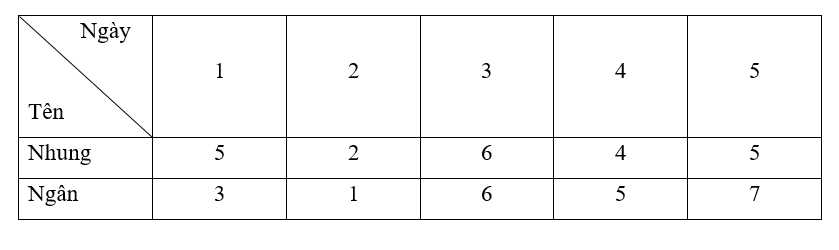
- Số giờ trung bình sử dụng Internet của bạn Nhung là:
Công thức tính phương sai của một mẫu số liệu là:
S2 =
Thay số ta có:
= [(5 – 4,4)2 + (2 – 4,4)2 + (6 – 4,4)2 + (4 – 4,4)2 + (5 – 4,4)2] = 1,84.
Do đó phương sai của mẫu số liệu trên là 1,84.
Độ lệch chuẩn của mẫu số liệu trên là S1 = = ≈ 1,36.
- Số giờ trung bình sử dụng Internet của bạn Ngân là:
Công thức tính phương sai của một mẫu số liệu là:
S2 =
Thay số ta có:
= [(3 – 4,4)2 + (1 – 4,4)2 + (6 – 4,4)2 + (5 – 4,4)2 + (7 – 4,4)2] = 4,64.
Do đó phương sai của mẫu số liệu trên là 4,64.
Độ lệch chuẩn của mẫu số liệu trên là S2 = = ≈ 2,15.
Ta thấy phương sai và độ lệch chuẩn trong số giờ sử dụng Internet của bạn Nhung bé hơn Ngân nên số giờ sử dụng Internet của bạn Nhung ổn định hơn.
Câu 2
Lời giải
Hướng dẫn giải:
Đáp án đúng là: B.
- Sắp xếp số lượng học sinh đạt giải của trường A theo thứ tự không giảm ta có:
6; 8; 10; 12; 15; 21.
+ Giá trị nhỏ nhất của mẫu số liệu trên là 6.
+ Giá trị lớn nhất của mẫu số liệu trên là 21.
Suy ra khoảng biến thiên RA = 21 – 6 = 15.
Ta lại có:
+ Giá trị tứ phân vị thứ nhất là trung vị của mẫu: 6; 8; 10.
Do đó Q1A = 8.
+ Giá trị tứ phân vị thứ ba là trung vị của mẫu: 12; 15; 21.
Do đó Q3A = 15.
Suy ra khoảng tứ phân vị ∆QA = Q3A – Q1A = 15 – 8 = 7.
- Sắp xếp số lượng học sinh đạt giải của trường B theo thứ tự không giảm ta có:
11; 15; 15; 17; 21; 23.
+ Giá trị nhỏ nhất của mẫu số liệu trên là 11
+ Giá trị lớn nhất của mẫu số liệu trên là 23
Suy ra khoảng biến thiên RB = 23 – 11 = 12.
Ta lại có:
+ Giá trị tứ phân vị thứ nhất là trung vị của mẫu: 11; 15; 15.
Do đó Q1B = 15.
+ Giá trị tứ phân vị thứ ba là trung vị của mẫu: 17; 21; 23.
Do đó Q3B = 21.
Suy ra khoảng tứ phân vị ∆QB = Q3B – Q1B = 21 – 15 = 6
Ta thấy khoảng biến thiên và khoảng tứ phân vị trong số lượng học sinh đạt giải của trường B bé hơn trường A nên số lượng đạt giải của trường B ổn định hơn.
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
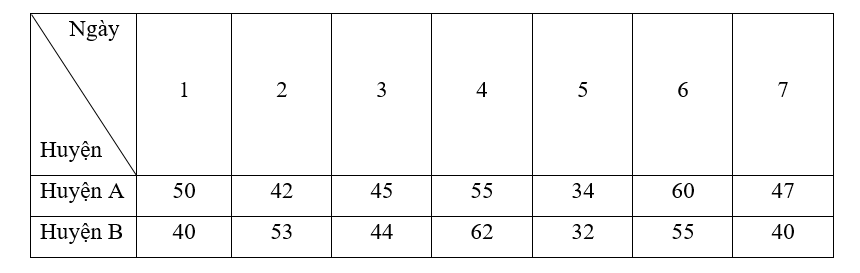
A. Huyện A;
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.