Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB = a, BC = 2a, AC' = a. Điểm N thuộc cạnh BB’ sao cho BN = 2NB', điểm M thuộc cạnh DD’ sao cho D'M = 2MD. Mp(A'MN) chia hình hộp chữ nhật làm hai phần, tính thể tích phần chứa điểm C'.
A. 4
B.
C. 2
D. 3
Quảng cáo
Trả lời:
Đáp án là C
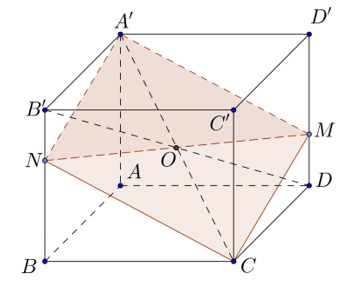
Nhận xét: B'NDM là hình bình hành (B'N = DM, B'N//DM)
=> MNB'D = O là trung điểm của mỗi đoạn nên O cũng là trung điểm của đường chéo A'C.
Vậy thiết diện tạo bởi mặt (A'MN) và hình chóp là hình bình hành A'NCM.
Ta có: ![]()
Cách 1:
Thể tích phần chứa C' là
![]()
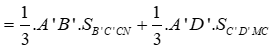
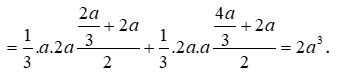
Cách 2: Áp dụng công thức tính nhanh
Gọi thể tích phần chứa C' là V'.
Ta có: 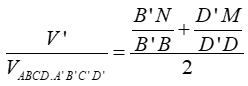
![]()
Cách 3: Nhận xét nhanh do đa diện chứa C' đối xứng với đa diện không chứa C' qua O nên thể tích của hai phần này bằng nhau, suy ra 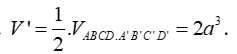
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A.
B. a
C. a
D. 2a
Lời giải
Chọn B.
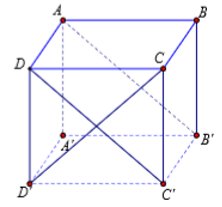
Do AB'//CD' => AB'//(DCC'D'). Suy ra
![]()
![]()
Lời giải
Đáp án là C
Gọi chiều rộng của đáy là x (cm) (x > 0)
Khi đó chiều cao của hố ga là 2x và chiều dài của hố ga là 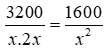
Diện tích xung quanh hố ga là 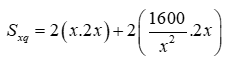
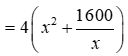
Diện đáy của hố ga là 
Tổng diện tích xây hố ga đó là 
Để xây tiết kiệm nguyên vật liệu nhất thì S phải nhỏ nhất.
Áp dụng bất đẳng thức Cô-Si ta có

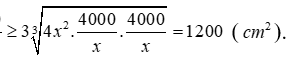
Dấu bằng xảy ra khi và chỉ khi ![]()
Khi đó diện tích đáy của hố ga là 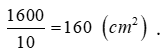
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. V = 3
B. V = 6
C. V = 2
D. V = 9
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. d = 4
B. d = 2
C. d =
D. d =
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. V = 12
B. V = 6
C. V = 2
D. V = 9
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.