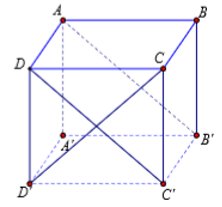
Cho hình lập phương ABCD.A'B'C'D' cạnh a. Gọi M, N lần lượt là trung điểm của BC và DD'. Tính theo a khoảng cách giữa hai đường thẳng MN và BD.
A. a
B.
C.
D.
Quảng cáo
Trả lời:
Chọn D.
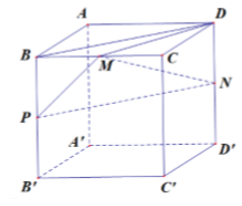
Gọi P là trung điểm BB’. Ta có BD//PN => BD//(MPN). Do đó:
d(MN;BD) = d(BD;(MPN)) = d(B;(MPN))
![]()
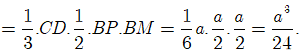
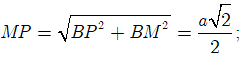
![]()
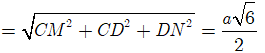
Nhận thấy ![]() nên tam giác MPN vuông tại M.
nên tam giác MPN vuông tại M.
Do đó 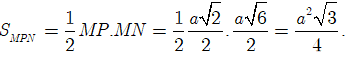
Ta có ![]()
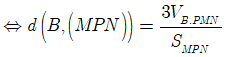
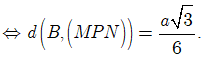
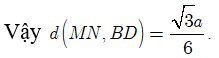
Cách 2:

Gọi P là trung điểm BB’. Ta có BD//PN => BD//(MPN).
Đồng thời, MP//CB', PN//B'D' => (MPN)//(CB'D')
Do đó ![]()
![]()
(vì PC’ cắt B’C tại trọng tâm tam giác BB’C’).
Nhận thấy tứ diện C'.CB'D' là tứ diện vuông tại C' nên
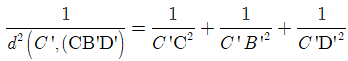
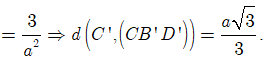
Vậy ![]()
Cách 3: Tọa độ hóa
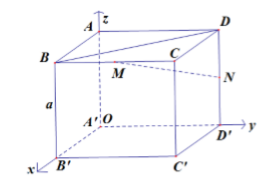
Chọn hệ trục tọa độ Oxyz như hình vẽ. Khi đó,
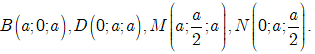
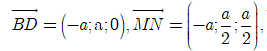
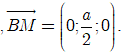
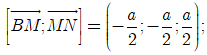
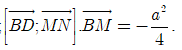
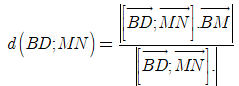
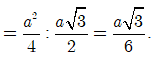
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A.
B. a
C. a
D. 2a
Lời giải
Chọn B.
Do AB'//CD' => AB'//(DCC'D'). Suy ra
![]()
![]()
Lời giải
Đáp án là C
Gọi chiều rộng của đáy là x (cm) (x > 0)
Khi đó chiều cao của hố ga là 2x và chiều dài của hố ga là 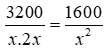
Diện tích xung quanh hố ga là 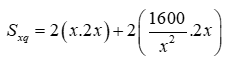
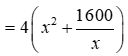
Diện đáy của hố ga là 
Tổng diện tích xây hố ga đó là 
Để xây tiết kiệm nguyên vật liệu nhất thì S phải nhỏ nhất.
Áp dụng bất đẳng thức Cô-Si ta có

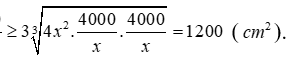
Dấu bằng xảy ra khi và chỉ khi ![]()
Khi đó diện tích đáy của hố ga là 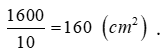
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. V = 3
B. V = 6
C. V = 2
D. V = 9
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. d = 4
B. d = 2
C. d =
D. d =
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. V = 12
B. V = 6
C. V = 2
D. V = 9
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.