Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SAD là tam giác đều và nằm trong mặt phẳng vuông góc với (ABCD). Gọi M, N, P lần lượt là tủng điểm các cạnh SB, BC, CD. Tính thể tích khối tứ diện CMNP.
A.
B.
C.
D.
Quảng cáo
Trả lời:
Chọn B.
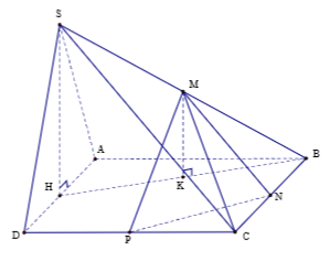
Gọi H là trung điểm của cạnh AD. Do tam giác SAD đều nên SHAD
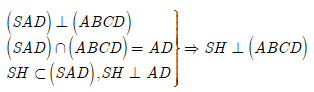
Gọi K là trung điểm của HB => MK//SH
Do đó: MKABCD => MK(CNP).
Vậy MK là chiều cao của khối tứ diện CMNP.
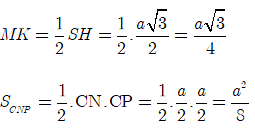
Thể tích khối tứ diện CMNP là
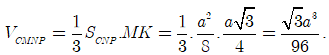
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A.
B. a
C. a
D. 2a
Lời giải
Chọn B.
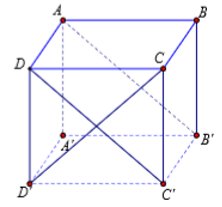
Do AB'//CD' => AB'//(DCC'D'). Suy ra
![]()
![]()
Lời giải
Đáp án là C
Gọi chiều rộng của đáy là x (cm) (x > 0)
Khi đó chiều cao của hố ga là 2x và chiều dài của hố ga là 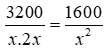
Diện tích xung quanh hố ga là 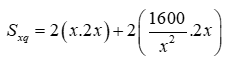
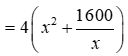
Diện đáy của hố ga là 
Tổng diện tích xây hố ga đó là 
Để xây tiết kiệm nguyên vật liệu nhất thì S phải nhỏ nhất.
Áp dụng bất đẳng thức Cô-Si ta có

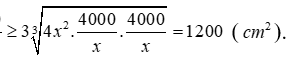
Dấu bằng xảy ra khi và chỉ khi ![]()
Khi đó diện tích đáy của hố ga là 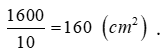
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. V = 3
B. V = 6
C. V = 2
D. V = 9
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. d = 4
B. d = 2
C. d =
D. d =
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. V = 12
B. V = 6
C. V = 2
D. V = 9
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.