Điểm dừng xe
Xét bài toán: Các điểm dừng đón, trả khách của xe buýt cách đều nhau một đoạn k mét. Điểm dừng đầu tiên ở đầu phố. Như vậy tính từ đầu phố, xe buýt dừng ở các điểm 0, k, 2k, 3k, ... (mét). Nhà của Tâm ở ngay đầu phố. Để kết hợp rèn luyện thể lực, Tâm thường đi bộ tới trường. Hôm nay, khi đi bộ được n mét, Tâm chợt nhớ cần phải tới sớm theo lời hẹn với một người bạn nên quyết định sẽ bắt xe buýt ở trạm tiếp theo gần nhất. Hãy xác định Tâm còn phải đi thêm bao nhiêu mét nữa.
Em hãy lập trình giải bài toán trên. Trước khi lập trình cần tóm tắt bài toán, xác định thuật toán và cách tổ chức dữ liệu.
Dữ liệu: Nhập vào từ thiết bị vào chuẩn, dòng đầu tiên chứa số nguyên k, dòng thứ hai chứa số nguyên n (1 ≤ k, n ≤ 2×109).
Kết quả: Đưa ra thiết bị ra chuẩn một số nguyên là độ dài đoạn đường cần đi tiếp (tính theo mét).
Ví dụ:
Input
Output
800
2 100
300
Điểm dừng xe
Xét bài toán: Các điểm dừng đón, trả khách của xe buýt cách đều nhau một đoạn k mét. Điểm dừng đầu tiên ở đầu phố. Như vậy tính từ đầu phố, xe buýt dừng ở các điểm 0, k, 2k, 3k, ... (mét). Nhà của Tâm ở ngay đầu phố. Để kết hợp rèn luyện thể lực, Tâm thường đi bộ tới trường. Hôm nay, khi đi bộ được n mét, Tâm chợt nhớ cần phải tới sớm theo lời hẹn với một người bạn nên quyết định sẽ bắt xe buýt ở trạm tiếp theo gần nhất. Hãy xác định Tâm còn phải đi thêm bao nhiêu mét nữa.
Em hãy lập trình giải bài toán trên. Trước khi lập trình cần tóm tắt bài toán, xác định thuật toán và cách tổ chức dữ liệu.
Dữ liệu: Nhập vào từ thiết bị vào chuẩn, dòng đầu tiên chứa số nguyên k, dòng thứ hai chứa số nguyên n (1 ≤ k, n ≤ 2×109).
Kết quả: Đưa ra thiết bị ra chuẩn một số nguyên là độ dài đoạn đường cần đi tiếp (tính theo mét).
Ví dụ:
|
Input |
Output |
|
800 2 100 |
300 |
Quảng cáo
Trả lời:
Tóm tắt bài toán (Mô hình toán học)
Cho:
- Các điểm (được đánh dấu) cách đều nhau k mét.
- Điểm đầu có toạ độ là 0.
- Điểm x có toạ độ là n.
Yêu cầu: Xác định khoảng cách gần nhất từ điểm x tới một điểm được đánh dấu.
Thuật toán và cách tổ chức dữ liệu:
- Bước 1. Nhập số nguyên k và n.
- Bước 2. Tính d là khoảng cách từ x tới điểm bên trái của x.
- Bước 3. Tìm min của khoảng cách từ x tới điểm bên trái x và bên phải của x.
- Bước 4. Đưa ra kết quả.
Tham khảo chương trình sau:

Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Trọng tâm Lí, Hóa, Sinh 10 cho cả 3 bộ KNTT, CTST và CD VietJack - Sách 2025 ( 40.000₫ )
- Sách - Sổ tay kiến thức trọng tâm Vật lí 10 VietJack - Sách 2025 theo chương trình mới cho 2k9 ( 31.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Tóm tắt bài toán (Mô hình toán học)
Cho: Dãy A gồm n số nguyên.
Yêu cầu: Đưa ra phân tử trung vị (phần tử nằm ở giữa dãy đã sắp xếp).
Thuật toán và chọn kiểu dữ liệu cho các biến
- Bước 1. Nhập số nguyên n, nhập danh sách A chứa n số nguyên.
- Bước 2. Sắp xếp danh sách A.
- Bước 3. Đưa ra phần tử A [len (A) //2].
Tham khảo chương trình sau:

Ví dụ một số bộ dữ liệu để kiểm thử chương trình:
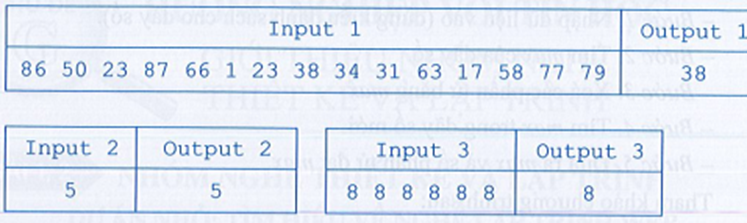
Lời giải
Tóm tắt bài toán (Mô hình toán học)
Cho: n và n - 1 số nguyên a1, a2, …, an-1 . Trong đó ai ≠ aj, với i ≠ j, với mọi i.
Yêu cầu: Tìm số bị thiếu không vượt quá n.
Thuật toán và cách tổ chức dữ liệu
- Nếu có đầy đủ n số thì tổng các số sẽ là
- Vậy số còn thiếu là:
- Không cần phải dùng dãy để lưu các số nhập vào.
- Các bước của thuật toán:
+ Bước 1. Nhập n.
+ Bước 2. Nhập và tính tổng các ai
+ Bước 3. Đưa ra kết quả.
Tham khảo chương trình sau:

Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
