Giải SBT Tin 10 Bài 17, 18. Thực hành lập trình giải bài toán trên máy tính có đáp án
42 người thi tuần này 4.6 753 lượt thi 5 câu hỏi
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Bộ 2 đề thi giữa kì 2 Tin học 10 Kết nối tri thức có đáp án - Đề 2
Bộ 2 đề thi giữa kì 2 Tin học 10 Kết nối tri thức có đáp án - Đề 1
Bộ 2 đề thi giữa kì 2 Tin học 10 Cánh diều có đáp án - Đề 2
Bộ 2 đề thi giữa kì 2 Tin học 10 Cánh diều có đáp án - Đề 1
Bộ 2 đề thi cuối kì 2 Tin học 10 Cánh diều có đáp án - Đề 2
Bộ 2 đề thi cuối kì 2 Tin học 10 Cánh diều có đáp án - Đề 1
Bộ 2 đề thi cuối kì 2 Tin học 10 Kết nối tri thức có đáp án - Đề 2
Bộ 2 đề thi cuối kì 2 Tin học 10 Kết nối tri thức có đáp án - Đề 1
Danh sách câu hỏi:
Lời giải
Tóm tắt bài toán (Mô hình toán học)
Cho:
- Số nguyên n, (1 105) và n số nguyên a1, a2, .., an (0 ≤ ai ≤104, i = 1, 2, .., n).
Yêu cầu:
- Xác định k là số lượng ai lớn hơn 0 và chia hết cho 3.
- Tính tổng (ai – 3)/3 với các ai tìm được.
Thuật toán và cách tổ chức dữ liệu
- Bước 1. Nhập dữ liệu vào (dùng kiểu danh sách cho dãy n số nguyên).
- Bước 2. Chuẩn bị tích luỹ số lượng và tổng: k = 0, s = 0.
- Bước 3. Duyệt với mọi i: Nếu ai > 0 và ai chia hết cho 3 thì tăng k và tích luỹ ai vào s.
- Bước 4. Đưa ra k và (s - 3k)/3.
Tham khảo chương trình sau:

Lời giải
Tóm tắt bài toán (Mô hình toán học)
Cho:
- Các điểm (được đánh dấu) cách đều nhau k mét.
- Điểm đầu có toạ độ là 0.
- Điểm x có toạ độ là n.
Yêu cầu: Xác định khoảng cách gần nhất từ điểm x tới một điểm được đánh dấu.
Thuật toán và cách tổ chức dữ liệu:
- Bước 1. Nhập số nguyên k và n.
- Bước 2. Tính d là khoảng cách từ x tới điểm bên trái của x.
- Bước 3. Tìm min của khoảng cách từ x tới điểm bên trái x và bên phải của x.
- Bước 4. Đưa ra kết quả.
Tham khảo chương trình sau:

Lời giải
Tóm tắt bài toán (Mô hình toán học)
Cho: n và n - 1 số nguyên a1, a2, …, an-1 . Trong đó ai ≠ aj, với i ≠ j, với mọi i.
Yêu cầu: Tìm số bị thiếu không vượt quá n.
Thuật toán và cách tổ chức dữ liệu
- Nếu có đầy đủ n số thì tổng các số sẽ là
- Vậy số còn thiếu là:
- Không cần phải dùng dãy để lưu các số nhập vào.
- Các bước của thuật toán:
+ Bước 1. Nhập n.
+ Bước 2. Nhập và tính tổng các ai
+ Bước 3. Đưa ra kết quả.
Tham khảo chương trình sau:

Lời giải
Tóm tắt bài toán (Mô hình toán học)
Cho: Dãy A gồm n số nguyên.
Yêu cầu: Đưa ra phân tử trung vị (phần tử nằm ở giữa dãy đã sắp xếp).
Thuật toán và chọn kiểu dữ liệu cho các biến
- Bước 1. Nhập số nguyên n, nhập danh sách A chứa n số nguyên.
- Bước 2. Sắp xếp danh sách A.
- Bước 3. Đưa ra phần tử A [len (A) //2].
Tham khảo chương trình sau:

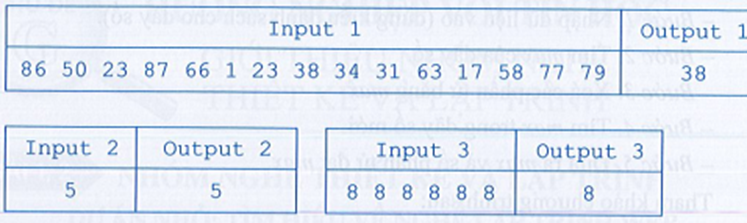
Ví dụ một số bộ dữ liệu để kiểm thử chương trình:
Lời giải
Tóm tắt bài toán (Mô hình toán học)
Cho n số thực dương dương g1, g2, …, gn.
Yêu cầu: tìm giá trị lớn thứ hai của dãy số và số phần tử đạt giá trị này.
Thuật toán 1 và cách tổ chức dữ liệu
- Bước 1. Nhập dữ liệu, lưu theo chỉ số bắt đầu từ 0 (dùng kiểu danh sách để chứa dãy số).
- Bước 2. Sắp xếp dãy số theo thứ tự giảm dần.
- Bước 3. Đếm số phần tử đạt max → k.
- Bước 4. Đếm số phần tử có giá trị đạt gk
- Bước 5. Đưa ra các giá trị tìm được.
Tham khảo chương trình sau:

Nhận xét: Chương trình trên đơn giản nhưng mất nhiều thời gian thực hiện vì phải sắp xếp
Thuật toán 2 và cách tổ chức dữ liệu
- Bước 1. Nhập dữ liệu vào (dùng kiểu danh sách cho dãy số).
- Bước 2. Tìm max của dãy số.
- Bước 3. Xoá các phần tử bằng max.
- Bước 4. Tìm max trong dãy số mới.
- Bước 5. Đưa ra max và số phần tử đạt max.
Tham khảo chương trình sau:

Ví dụ một số bộ dữ liệu để kiểm thử chương trình:

