Cho hình chóp S.ABC, M và N là các điểm thuộc các cạnh SA và SB sao cho MA= 2SM, SN = 2NB, là mặt phẳng qua MN và song song với SC. Kí hiệu (H1) và (H2) là các khối đa diện có được khi chia khối chóp S.ABC bới mặt phẳng trong đó (H1) chứa điểm S, (H2) chứa điểm A; V1 và V2 lần lượt là thể tích của (H1) và (H2). Tính tỉ số
A.
B.
C.
D.
Quảng cáo
Trả lời:
Chọn D.
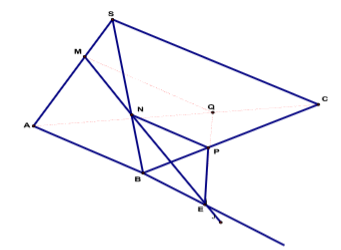
Mp () qua MN và song song với SC. Mp () cắt BC và cắt AC tại P và Q ta có:
NP // SC nên ![]() Ta có: MN, PQ, AB đồng quy tại E.
Ta có: MN, PQ, AB đồng quy tại E.
Áp dụng định lí Mennelauyt trong tam giác SAB, ta có:
![]()
![]()
Áp dụng định lí Menelauyt trong tam giác ABC ta có: ![]()
![]()
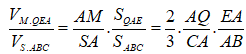
![]()
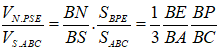
![]()
![]()
![]()
![]()
Vậy 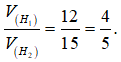
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. V =
B. V =
C. V =
D. V =
Lời giải
Chọn A.
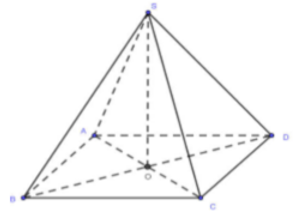
![]()
Gọi ![]()
![]()
![]()
![]()
Lời giải
Chọn B.
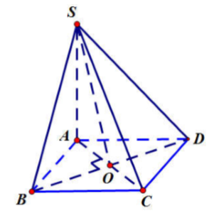
Gọi O = ACBD. Vì ABCD là hình thoi nên BOAC(1). Lại do:
![]()
Từ (1) và (2) ta có:BO(SAC)
![]()
Ta có: ![]()
Vì ABCD là hình thoi có ABC = 60 nên tam giác ABC đều cạnh a
![]()
Trong tam giác vuông SBO ta có:
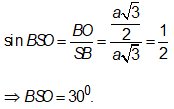
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.