Có ba nhóm máy A, B, C dùng để sản xuất ra hai loại sản phẩm I và II. Để sản xuất một đơn vị sản phẩm mỗi loại phải lần lượt dùng các máy thuộc các nhóm khác nhau. Số máy trong một nhóm và số máy của từng nhóm cần thiết để sản xuất ra một đơn vị sản phẩm thuộc mỗi loại được cho trong bảng sau:
|
Nhóm |
Số máy trong mỗi nhóm |
Số máy trong từng nhóm để sản xuất ra một đơn vị sản phẩm |
|
|
Loại I |
Loại II |
||
|
A |
10 |
2 |
2 |
|
B |
4 |
0 |
2 |
|
C |
12 |
2 |
4 |
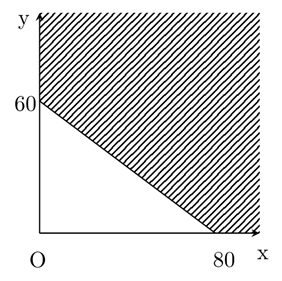
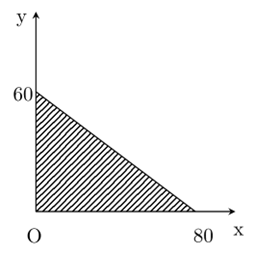
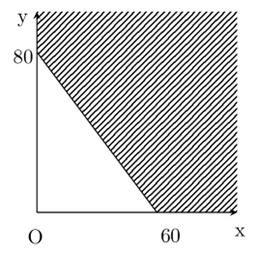
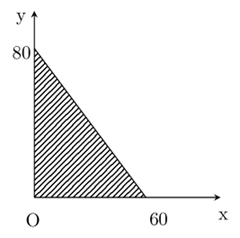
Gọi x, y (x, y ≥ 0) lần lượt là số đơn vị sản phẩm loại I và loại II sản xuất. Các bất phương trình mô tả số đơn vị sản phẩm loại I và loại II sản xuất là:
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hướng dẫn giải
Đáp án đúng là: D
Để sản xuất một đơn vị sản phẩm loại I thì cần 2 máy nhóm A và 2 máy nhóm C nên để sản xuất x đơn vị sản phẩm loại I thì cần 2x máy nhóm A và 2x máy nhóm C.
Để sản xuất một đơn vị sản phẩm loại II thì cần 2 máy nhóm A, 2 máy nhóm B và 4 máy nhóm C nên để sản xuất y đơn vị sản phẩm loại II thì cần 2y máy nhóm A, 2y máy nhóm B và 4y máy nhóm C.
Mà có tất cả 10 máy nhóm A nên ta có: 2x + 2y ≤ 10 Û x + y – 5 ≤ 0.
Có tất cả 4 máy nhóm B nên ta có: 2y ≤ 4 Û y ≤ 2.
Có tất cả 12 máy nhóm C nên ta có: 2x + 4y ≤ 12 Û x + 2y – 6 ≤ 0.
Vậy ta có các bất phương trình:
x ≥ 0;
0 ≤ y ≤ 2;
x + y – 5 ≤ 0;
x + 2y – 6 ≤ 0.
Ta chọn phương án D.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Hướng dẫn giải
Đáp án đúng là: D
Thời gian tối đa để hoàn thiện:
+ Kệ sách là: 240 : 4 = 60 giờ.
+ Bàn: 240 : 3 = 80 giờ.
Khi đó ta có:
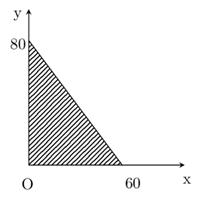
Câu 2
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Hướng dẫn giải
Đáp án đúng là: D
Do điểm A(\(\sqrt 2 \); 1) thuộc miền nghiệm của bất phương trình, thay x = \(\sqrt 2 \) và y = 1 vào bất phương trình ta được:
\(3\sqrt 2 + m - 7 \ge 0 \Leftrightarrow m \ge 7 - 3\sqrt 2 \)
Vậy với \(m \in \left[ {7 - 3\sqrt 2 ; + \infty } \right)\) thì bất phương trình 3x + my − 7 ≥ 0 có miền nghiệm chứa điểm A(\(\sqrt 2 \); 1).
Ta chọn phương án D.
Câu 3
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập