Trong mặt phẳng tọa độ Oxy, cho đồ thị hàm số y = f(x) = x2
1) Tính f(−1); f(3).
2) Cho A(−1; 1), B(3; 9) nằm trên đồ thị hàm y = x2. Gọi M là điểm thay đổi trên đồ thị hàm số y = x2 và có hoành độ là m (−1 < m < 3). Tìm m để tam giác ABM có diện tích lớn nhất.
Trong mặt phẳng tọa độ Oxy, cho đồ thị hàm số y = f(x) = x2
1) Tính f(−1); f(3).
2) Cho A(−1; 1), B(3; 9) nằm trên đồ thị hàm y = x2. Gọi M là điểm thay đổi trên đồ thị hàm số y = x2 và có hoành độ là m (−1 < m < 3). Tìm m để tam giác ABM có diện tích lớn nhất.
Câu hỏi trong đề: Đề thi Học kì 2 Toán 9 chọn lọc, có đáp án !!
Quảng cáo
Trả lời:
1) + f(−1)
Thay x = −1 vào y = x2, ta được: f(−1) = (−1)2 = 1.
+ f(3)
Thay x = 3 vào y = x2, ta được: f(3) = 32 = 9.
Vậy f( – 1) = 1 và f(3) = 9.
2) Kẻ AH, MK, BI lần lượt vuông góc với Ox tại H, M, I ta được hình vẽ sau:
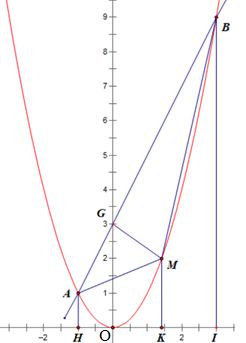
Khi đó AH = |yA| = 1; OH = |xA| = |-1| = 1;
OK = |xM| = |m|; MK = |yM| = m2;
OI = |xB| = 3; BI = |yB| = 9.
Suy ra: HK = |m + 1|; KI = OI – OK = |3 – m|;
HI = OH + OI = 1 + 3 = 4.
Ta có: S∆ABM = SAHIB – SAHKM – SMKIB
Ta có: Tứ giác AHIB, AHKM, MKIB là những hình thang vuông nên:
SAHIB = (AH + BI). HI = (1 + 9).4 = 20 (đvdt).
SAMKH = (AH + MK). HK = (1 + |yM|).|xM + 1| = (1 + m2).|m + 1|
SMKIB = (MK + BI). KI = (m2 + 9). |3 – m|
Þ SABM = 20 − (1 + m2).|m + 1| − (m2 + 9). |3 – m|
Do −1 < m < 3 nên , ∀m Î (−1;3)
Khi đó: SABM = 20 − ![]() (1 + m2).(m + 1) −
(1 + m2).(m + 1) − ![]() (m2 + 9). (3 – m)
(m2 + 9). (3 – m)
= 20 − (m + 1 + m3 + m2) − (3m2 – m3 + 27 – 9m)
= 20 − (4m2 – 8m + 28)
Để diện tích của tam giác ABM đạt GTLN thì (4m2 – 8m + 28) đạt GTNN
Mà (4m2 – 8m + 28) = 4(m2 – 2m + 7) = 4(m2 – 2m + 1) + 24 = 4(m – 1)2 + 24 ≥ 24, ∀m
Dấu “=” xảy ra khi m = 1.
Vậy (4m2 – 8m + 28) đạt GTNN bằng 24 khi m = 1.
Vậy S∆ABM đạt GTLN bằng 8 khi m = 1.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án đúng là: D

Gọi O là tâm của hình vuông ABCD, E; F; K; G lần lượt là trung điểm của AD, DC, BC, AB.
Khi đó ta có OE = OF = OK = OG = ![]() . Hay O là tâm đường tròn nội tiếp hình vuông ABCD.
. Hay O là tâm đường tròn nội tiếp hình vuông ABCD.
Vậy bán kính đường tròn nội tiếp hình vuông là R = ![]() .
.
Câu 2
Lời giải
Đáp án đúng là: D
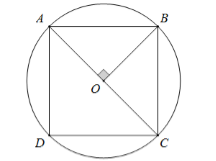
Hình vuông ABCD nội tiếp đường tròn (O), O là tâm của hình vuông ABCD.
Vì ABCD là hình vuông nên 2 đường chéo vuông góc với nhau đồng thời chúng bằng nhau và cắt nhau tại trung điểm của mỗi đường Þ OA ^ OB và OA = OB.
Þ ∆OAB vuông cân tại O.
Gọi R là bán kính của đường tròn ngoại tiếp (O), ta có
AC = AB= 8 Þ R = = = cm.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
C. = 180°.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.