Câu hỏi:
25/08/2022 253Cho biết \(2\cos \alpha + \sqrt 2 \sin \alpha = 2\), với 0° < α < 90°. Giá trị của cotα bằng:
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hướng dẫn giải
Đáp án đúng là: D
Ta có \(2\cos \alpha + \sqrt 2 \sin \alpha = 2\)
\[ \Leftrightarrow \sqrt 2 \sin \alpha = 2 - 2\cos \alpha \]
⇒ 2sin2α = (2 – 2cosα)2
⇔ 2(1 – cos2α) = 4 – 8cosα + 4cos2α
⇔ 6cos2α – 8cosα + 2 = 0 (1)
Đặt t = cosα.
Vì 0° < α < 90° nên 0 < t < 1.
Phương trình (1) tương đương với: 6t2 – 8t + 2 = 0
\( \Leftrightarrow \left[ \begin{array}{l}t = 1\\t = \frac{1}{3}\end{array} \right.\)
Vì 0 < t < 1 nên ta nhận \(t = \frac{1}{3}\).
Với \(t = \frac{1}{3}\), ta có \[\cos \alpha = \frac{1}{3}\].
Suy ra \[{\cos ^2}\alpha = \frac{1}{9}\]
Áp dụng Bài tập 5a, trang 65, Sách giáo khoa Toán 10, Tập một, ta có:
sin2α + cos2α = 1
\[ \Leftrightarrow {\sin ^2}\alpha = 1 - {\cos ^2}\alpha = 1 - \frac{1}{9} = \frac{8}{9}\].
\( \Leftrightarrow \left[ \begin{array}{l}\sin \alpha = \frac{{2\sqrt 2 }}{3}\\\sin \alpha = - \frac{{2\sqrt 2 }}{3}\end{array} \right.\)
Vì 0° < α < 90° nên α là góc nhọn.
Do đó sinα > 0.
Vì vậy ta nhận \(\sin \alpha = \frac{{2\sqrt 2 }}{3}\).
Ta có \(\cot \alpha = \frac{{\cos \alpha }}{{\sin \alpha }} = \frac{1}{3}:\frac{{2\sqrt 2 }}{3} = \frac{1}{3}.\frac{3}{{2\sqrt 2 }} = \frac{1}{{2\sqrt 2 }} = \frac{{\sqrt 2 }}{4}\).
Vậy ta chọn phương án D.
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
- Trọng tâm Lí, Hóa, Sinh 10 cho cả 3 bộ KNTT, CTST và CD VietJack - Sách 2025 ( 40.000₫ )
- Trọng tâm Toán, Văn, Anh 10 cho cả 3 bộ KNTT, CTST, CD VietJack - Sách 2025 ( 13.600₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải
Đáp án đúng là: D
⦁ Ta xét khẳng định (I):
Áp dụng định lí côsin cho ∆ABC ta có:
b2 – c2 = c2 + a2 – 2ca.cosB – (a2 + b2 – 2ab.cosC)
= c2 + a2 – 2ca.cosB – a2 – b2 + 2ab.cosC
= c2 – b2 + 2a(b.cosC – c.cosB)
Þ b2 – c2 = c2 – b2 + 2a(b.cosC – c.cosB)
Þ 2(b2 – c2) = 2a(b.cosC – c.cosB)
Þ b2 – c2 = a(b.cosC – c.cosB).
Do đó khẳng định (I) đúng.
⦁ Ta xét khẳng định (II):
Áp dụng hệ quả định lí sin cho ∆ABC ta có:
(b + c)sinA = \[\left( {2R.\sin B + 2R.\sin C} \right).\frac{a}{{2R}}\]
\[ = \left( {\sin B + \sin C} \right).\frac{{2R.a}}{{2R}}\]
= a(sinB + sinC).
Vì vậy khẳng định (II) đúng.
⦁ Ta xét khẳng định (III):
Áp dụng hệ quả định lí sin cho ∆ABC ta có:
2R.sinB.sinC = \(2R.\frac{b}{{2R}}.\frac{c}{{2R}}\)
\( = \frac{{bc}}{{2R}} = \frac{{abc}}{{4R}}.\frac{2}{a}\)
\( = \frac{{2S}}{a} = {h_a}\).
Vì vậy khẳng định (III) đúng.
⦁ Ta xét khẳng định (IV):
Áp dụng hệ quả định lí sin cho ∆ABC ta có:
R.r.(sinA + sinB + sin C) = \(R.r.\left( {\frac{a}{{2R}} + \frac{b}{{2R}} + \frac{c}{{2R}}} \right)\)
\[ = R.r.\frac{1}{R}\left( {\frac{a}{2} + \frac{b}{2} + \frac{c}{2}} \right)\]
\[ = r.\frac{{a + b + c}}{2} = r.p = S\].
Vì vậy khẳng định (IV) đúng.
Vậy có 4 khẳng định đúng, ta chọn phương án D.
Lời giải
Hướng dẫn giải
Đáp án đúng là: D
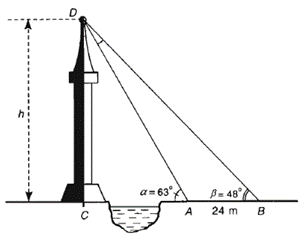
Ta có \(\widehat {CAD} + \widehat {BAD} = 180^\circ \) (hai góc kề bù).
\( \Rightarrow \widehat {BAD} = 180^\circ - \widehat {CAD} = 180^\circ - 63^\circ = 117^\circ \).
∆ABD có: \(\widehat {BAD} + \widehat {ADB} + \widehat {ABD} = 180^\circ \) (định lí tổng ba góc trong một tam giác)
\( \Rightarrow \widehat {ADB} = 180^\circ - \left( {\widehat {BAD} + \widehat {ABD}} \right) = 180^\circ - \left( {117^\circ + 48^\circ } \right) = 15^\circ \).
Áp dụng định lí sin cho ∆ABD, ta được \(\frac{{BD}}{{\sin \widehat {BAD}}} = \frac{{AB}}{{\sin \widehat {ADB}}}\)
Suy ra \(\frac{{BD}}{{\sin 117^\circ }} = \frac{{24}}{{\sin 15^\circ }}\)
Do đó \(BD = \frac{{24.\sin 117^\circ }}{{\sin 15^\circ }} \approx 82,6\) (m)
∆BCD vuông tại C: \(\sin \widehat {CBD} = \frac{{CD}}{{BD}}\).
Suy ra \(h = CD = BD.\sin \widehat {CBD} \approx 82,6.\sin 48^\circ = 61,4\) (m)
Giá trị này gần với 60,5 m.
Vậy ta chọn phương án D.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
13 câu Trắc nghiệm Tích của vectơ với một số có đáp án (Thông hiểu)
-
12 Bài tập Ứng dụng của hàm số bậc hai để giải bài toán thực tế (có lời giải)
-
16 câu Trắc nghiệm Toán 10 Kết nối tri thức Mệnh đề có đáp án
-
10 Bài tập Ứng dụng ba đường conic vào các bài toán thực tế (có lời giải)
-
10 Bài tập Tìm hệ số, số hạng trong khai triển nhị thức Newton (có lời giải)
-
Bộ 2 Đề kiểm tra giữa học kì 2 Toán 10 Kết nối tri thức có đáp án - Đề 1
-
10 Bài tập Cách xét tính đúng sai của mệnh đề (có lời giải)
-
10 Bài tập Cách xét tính đúng sai của mệnh đề (có lời giải)
Nhắn tin Zalo