Chứng minh rằng parabol (P): luôn cắt đường thẳng (d): tại hai điểm phân biệt A và B. Gọi là hoành độ hai điểm A, B. Tìm m sao cho
Chứng minh rằng parabol (P): luôn cắt đường thẳng (d): tại hai điểm phân biệt A và B. Gọi là hoành độ hai điểm A, B. Tìm m sao cho
Câu hỏi trong đề: Bộ đề Ôn tập Toán 9 thi vào 10 năm 2020 có đáp án !!
Quảng cáo
Trả lời:
Phương trình hoành độ giao điểm của P và d là:
Ta có
với mọi m
Suy ra phương trình 1 luôn có hai nghiệm phân biết với mọi m
Nên P luôn cắt d tại hai điểm phân biệt A và B
Theo vi-ét ta có:
Theo đề ta có:
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Bảng sau cho một số giá trị tương ứng của x và y

Vẽ đồ thị:
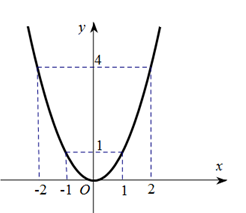
Lời giải
a)
Ta có bảng giá trị sau
|
x |
-2 |
-1 |
0 |
1 |
2 |
|
y |
2 |
|
0 |
|
2 |
Đồ thị hàm số là đường cong đi qua các điểm (-2;2); (-1; ); (0;0); (1; ); (2;2) và nhận trục Oy làm trục đối xứng.
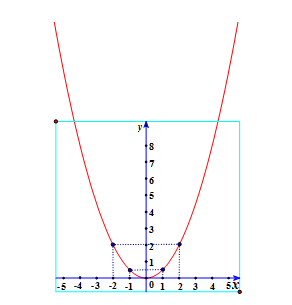
b) Xét phương trình hoành độ giao điểm của đồ thị hàm số (P) và đường thẳng (d):
Với x = 0 => y = 0 ta có giao điểm O(0;0)
Với x = 2 => y = 2 ta có giao điểm A(2;2)
Vậy giao điểm của đồ thị hàm số (P) và đường thẳng (d) là O(0;0); A(2;2)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.