ho phương trình: 2x2 – 3x – 8 = 0 có hai nghiệm x1; x2.
a) Không giải phương trình, hãy tính S = x1 + x2 và P = x1x2.
b) Tính:
ho phương trình: 2x2 – 3x – 8 = 0 có hai nghiệm x1; x2.
a) Không giải phương trình, hãy tính S = x1 + x2 và P = x1x2.
b) Tính:
Câu hỏi trong đề: Đề thi Học kì 2 Toán 9 chọn lọc, có đáp án !!
Quảng cáo
Trả lời:
a) Ta có phương trình 2x2 – 3x – 8 = 0 với a = 2, b = −3, c = −8.
Theo định lý Vi – ét, ta có:
S = x1 + x2 = = .
P = x1x2 = = = −4.
b) Ta có: =
=
= = .
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải

a) Ta có: = 90° (CF là đường cao)
= 90° (BE là đường cao)
Xét tứ giác BFEC có = 90°
Mà 2 đỉnh E, F kề nhau cùng nhìn cạnh BC dưới hai góc bằng nhau.
Vậy tứ giác BFEC nội tiếp.
b) Ta có BE, CF là đường cao trong ∆ABC và BE, CF cắt nhau tại H.
Khi đó, H là trực tâm ∆ABC nên AD là đường cao.
Do đó = 90°.
Xét ∆AHE và ∆ACD có:
là góc chung.
(= 90°).
Do đó ∆AHE ∆ACD (g.g).
Suy ra (cặp cạnh tương ứng).
Vậy AE.AC = AH.AD (đpcm).
c) Gọi Ax là tiếp tuyến đường tròn tâm O.
Ta có: (cùng chắn cung AC).
(tứ giác BFEC nội tiếp).
Hay
Mà
Suy ra mà
Do đó Þ EF // Ax
Mà Ax ^ OA(tiếp tuyến đường tròn tâm O) hay Ax ^ AK (AK là đường kính)
Suy ra EF ^ AK.
Ta có: AK ^ EF (chứng minh trên) mà MN ^ AK Þ EF // MN
Suy ra mà (cùng chắn cung BF).
Nên
Do đó .
Vậy HNDM nội tiếp (cùng nhìn cạnh ND dưới hai góc bằng nhau).
Lời giải
a) Vẽ (P)
Bảng giá trị:
|
x |
−2 |
−1 |
0 |
1 |
2 |
|
y = −x2 |
−4 |
−1 |
0 |
−1 |
−4 |
Trên mặt phẳng tọa độ lấy các điểm: A(−2; −4), B(−1; −1), O(0; 0), C(1; −1), D(2; −4).
Vẽ (D)
Đường thẳng (D): y = 2x – 3 có a = 2, b = −3 đi qua hai điểm có tọa độ (0; b) và
Do đó, hai điểm thuộc đường thẳng (D) là M(0; −3) và N .
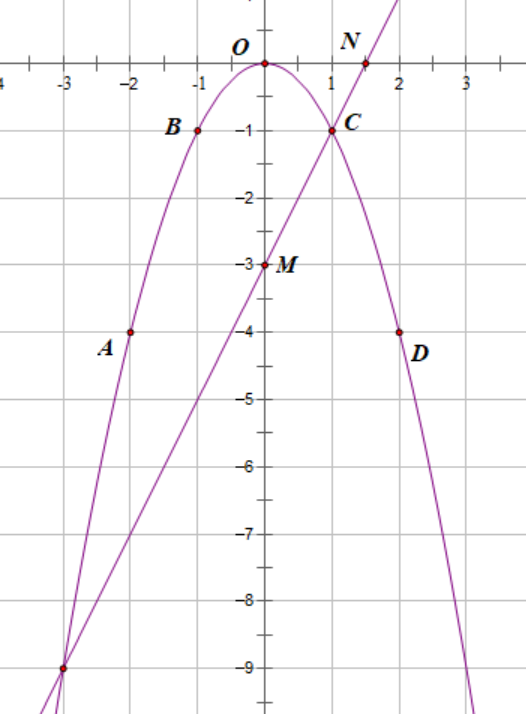
b) Phương trình hoành độ giao điểm của (P) và (D) là:
−x2 = 2x – 3
Û −x2 – 2x + 3 = 0
Û x2 + 2x – 3 = 0
Û x2 – x + 3x – 3 = 0
Û x(x – 1) + 3(x – 1) = 0
Û (x+3)(x – 1) = 0
Û
• Với x = −3 thì y = 2x – 3 = 2 . (−3) – 3 = −9.
Do đó, ta có tọa độ giao điểm của (P) và (D) là E(−3; −9).
• Với x = 1 thì y = 2x – 3 = 2 . 1 – 3 = −1.
Do đó, ta có tọa độ giao điểm của (P) và (D) là F(1; −1).
Vậy đồ thị hàm số (P) và (D) có 2 giao điểm là E(−3; −9) và F(1; −1).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.