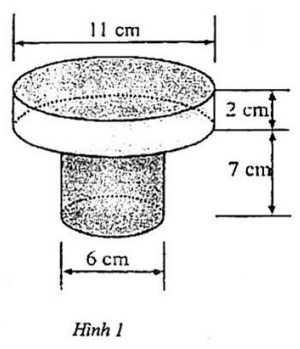
Một chi tiết máy có các kích thước như hình 1. Tính thể tích của chi tiết máy đó (làm tròn kết quả đến hàng đơn vị).

Câu hỏi trong đề: Đề thi Học kì 2 Toán 9 chọn lọc, có đáp án !!
Quảng cáo
Trả lời:
Thể tích phần cần tính là tổng thế tích của hai hình trụ có đường kính là 11 cm và chiều cao là 2 cm.
V1 = pR2.h1 = = 60,5p (cm3)
Thể tích hình trụ có đường kính đáy là 6 cm, chiều cao là 7 cm là:
V2 = pR2.h2 = = 63p (cm3)
Thể tích của chi tiết máy là:
V = V1 + V2 = 60,5p + 63p = 123,5p (cm3).
Ta có: 123,5p ≈ 388.
Vậy thể tích của chi tiết máy đó (làm tròn kết quả đến hàng đơn vị) là 388 cm3.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải

a) Ta có: = 90° (CF là đường cao)
= 90° (BE là đường cao)
Xét tứ giác BFEC có = 90°
Mà 2 đỉnh E, F kề nhau cùng nhìn cạnh BC dưới hai góc bằng nhau.
Vậy tứ giác BFEC nội tiếp.
b) Ta có BE, CF là đường cao trong ∆ABC và BE, CF cắt nhau tại H.
Khi đó, H là trực tâm ∆ABC nên AD là đường cao.
Do đó = 90°.
Xét ∆AHE và ∆ACD có:
là góc chung.
(= 90°).
Do đó ∆AHE ∆ACD (g.g).
Suy ra (cặp cạnh tương ứng).
Vậy AE.AC = AH.AD (đpcm).
c) Gọi Ax là tiếp tuyến đường tròn tâm O.
Ta có: (cùng chắn cung AC).
(tứ giác BFEC nội tiếp).
Hay
Mà
Suy ra mà
Do đó Þ EF // Ax
Mà Ax ^ OA(tiếp tuyến đường tròn tâm O) hay Ax ^ AK (AK là đường kính)
Suy ra EF ^ AK.
Ta có: AK ^ EF (chứng minh trên) mà MN ^ AK Þ EF // MN
Suy ra mà (cùng chắn cung BF).
Nên
Do đó .
Vậy HNDM nội tiếp (cùng nhìn cạnh ND dưới hai góc bằng nhau).
Lời giải
a) Vẽ (P)
Bảng giá trị:
|
x |
−2 |
−1 |
0 |
1 |
2 |
|
y = −x2 |
−4 |
−1 |
0 |
−1 |
−4 |
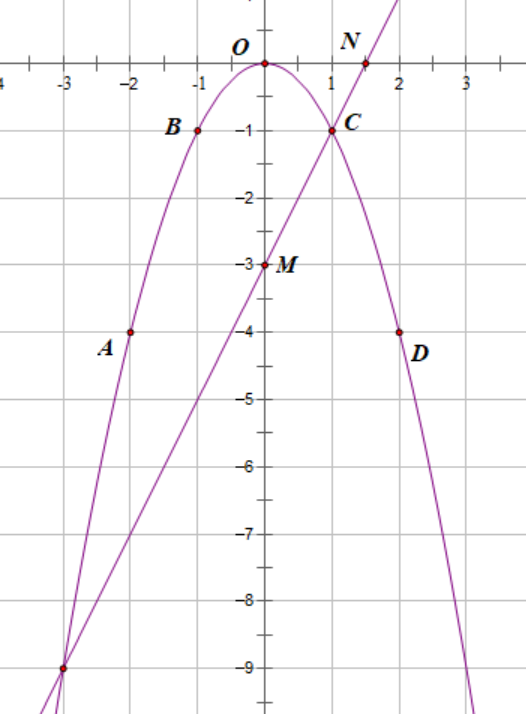
Trên mặt phẳng tọa độ lấy các điểm: A(−2; −4), B(−1; −1), O(0; 0), C(1; −1), D(2; −4).
Vẽ (D)
Đường thẳng (D): y = 2x – 3 có a = 2, b = −3 đi qua hai điểm có tọa độ (0; b) và
Do đó, hai điểm thuộc đường thẳng (D) là M(0; −3) và N .
b) Phương trình hoành độ giao điểm của (P) và (D) là:
−x2 = 2x – 3
Û −x2 – 2x + 3 = 0
Û x2 + 2x – 3 = 0
Û x2 – x + 3x – 3 = 0
Û x(x – 1) + 3(x – 1) = 0
Û (x+3)(x – 1) = 0
Û
• Với x = −3 thì y = 2x – 3 = 2 . (−3) – 3 = −9.
Do đó, ta có tọa độ giao điểm của (P) và (D) là E(−3; −9).
• Với x = 1 thì y = 2x – 3 = 2 . 1 – 3 = −1.
Do đó, ta có tọa độ giao điểm của (P) và (D) là F(1; −1).
Vậy đồ thị hàm số (P) và (D) có 2 giao điểm là E(−3; −9) và F(1; −1).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.