Cho tam giác ABC có . Các tia phân giác góc B, góc C cắt nhau tại O và cắt AC; AB theo thứ tự D; E. Chứng minh rằng: OD=OE.
Cho tam giác ABC có . Các tia phân giác góc B, góc C cắt nhau tại O và cắt AC; AB theo thứ tự D; E. Chứng minh rằng: OD=OE.
Quảng cáo
Trả lời:
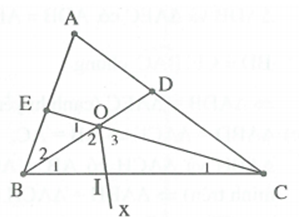
có
Mà nên .
Ta có .
có
Nên .
- Kẻ Ox là tia phân giác góc , cắt BC tại I nên .
Xét và có (giả thiết); ; BO là cạnh chung
do đó . Suy ra .
- Chứng minh tương tự ta có nên OD= OI.
Vậy .
* Nhận xét.
- Để chứng minh OE=OD, ta chưa thể ghép chúng vào hai tam giác nào bằng nhau được. Do vậy, ta nghĩ đến cách kẻ đường phụ. Cho số đo góc A ta liên hệ với bài đã biết nên tính được số đo góc BOC và góc BOE nên dựng được điểm I.
- Bài toán còn có cách khác, là lấy điểm I trên BC sao cho BI=BE, sau đó chứng minh rồi chứng minh .
- Từ cách trên ta còn suy ra kết quả đẹp là .
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
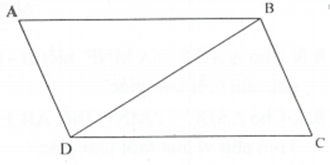
(cặp so le trong)
(cặp so le trong)
và có , BD là cạnh chung, .
Suy ra .
Lời giải
Hướng dẫn:
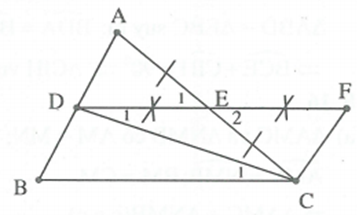
a) Ta dễ chứng minh được
Suy ra
Và , mà hai góc ở vị trí so le trong nên .
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.