Câu hỏ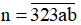i:
12/07/2024 1,076
Cho số 
. Hãy thay a, b bởi các chữ số thích hợp, biết n vừa chia hết cho 5, vừa chia hết cho 9.
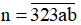. Hãy thay a, b bởi các chữ số thích hợp, biết n vừa chia hết cho 5, vừa chia hết cho 9.Câu hỏi trong đề: Giải SBT Toán lớp 6 KNTT Bài 9: Dấu hiệu chia hết có đáp án !!
Bắt đầu thiQuảng cáo
Trả lời:
Giải bởi Vietjack
Vì n chia hết cho 5 nên n có chữ số tận cùng là 0 hoặc 5. Do đó b = 0 hoặc b = 5
+) Với b = 0 ta được số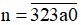 
Để n chia hết cho 9 thì (3 + 2 + 3 + a + 0) chia hết cho 9 hay (8 + a) chia hết cho 9.
Mà 0 ≤ a ≤ 9 nên a = 1. Ta được số cần tìm là 32 310.
+) Với b = 5 ta được số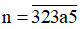 
Để n chia hết cho 9 thì (3 + 2 + 3 + a + 5) chia hết cho 9 hay (13 + a) chia hết cho 9.
Mà 0 ≤ a ≤ 9 nên a = 5. Ta được số cần tìm là 32 355.
Vậy cặp số (a; b) thỏa mãn là (1; 0); (5; 5).
Nhà sách vietjack
Hot: Đề thi cuối kì 2 Toán, Văn, Anh.... file word có đáp án chi tiết lớp 1-12 form 2025 (chỉ từ 100k). Tải ngay
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Chuẩn bị cho năm học mới, Mai được mẹ mua cho một số bút và một số quyển vở hết tất cả 165 nghìn đồng. Biết một chiếc bút giá 17 nghìn đồng, một quyển vở giá 5 nghìn đồng. Hỏi mẹ đã mua cho Mai bao nhiêu cái bút, bao nhiêu quyển vở?
Xem đáp án »
13/07/2024
5,470
Câu 2:
Không thực hiện phép tính, hãy cho biết tổng (hiệu) sau có chia hết cho 2 hay không.
a) 2 020 + 2 022; b) 20213 – 20203
Không thực hiện phép tính, hãy cho biết tổng (hiệu) sau có chia hết cho 2 hay không.
a) 2 020 + 2 022; b) 20213 – 20203
Xem đáp án »
13/07/2024
4,058
Câu 3:
Không thực hiện phép tính, hãy cho biết tổng (hiệu) sau có chia hết cho 5 hay không.
a) 2 020 + 2 021; b) 20255 – 20204
Không thực hiện phép tính, hãy cho biết tổng (hiệu) sau có chia hết cho 5 hay không.
a) 2 020 + 2 021; b) 20255 – 20204
Xem đáp án »
13/07/2024
2,475
Câu 4:
Lớp 6A muốn thành lập một nhóm nhảy để khi biểu diễn có thể tách ra đều thành từng nhóm 3 người hoặc nhóm 5 người. Hỏi nhóm nhảy cần ít nhất bao nhiêu người?
Xem đáp án »
13/07/2024
1,557
Câu 5:
Tổng sau có chia hết cho 3 hay không? Vì sao?
a) A = 1012 + 1;
b) B = 1012 + 3.
Tổng sau có chia hết cho 3 hay không? Vì sao?
a) A = 1012 + 1;
b) B = 1012 + 3.
Xem đáp án »
13/07/2024
1,312
Câu 6:
Dùng bốn số: 0; 2; 3; 5 để tạo ra các số có bốn chữ số, mỗi chữ số đã cho chỉ lấy một lần sao cho:
a) Các số đó chia hết cho 2
b) Các số đó chia hết cho 5
c) Các số đó chia hết cho cả 2 và 5.
Dùng bốn số: 0; 2; 3; 5 để tạo ra các số có bốn chữ số, mỗi chữ số đã cho chỉ lấy một lần sao cho:
a) Các số đó chia hết cho 2
b) Các số đó chia hết cho 5
c) Các số đó chia hết cho cả 2 và 5.
Xem đáp án »
12/07/2024
1,293
🔥 Đề thi HOT:
-
Đề kiểm tra Giữa kì 2 Toán 6 có đáp án (Mới nhất) - Đề 1
-
Đề thi Cuối học kì 2 Toán 6 có đáp án (Đề 1)
-
Dạng 4: Một số bài tập nâng cao về lũy thừa
-
31 câu Trắc nghiệm Toán 6 Kết nối tri thức Bài 1: Tập hợp có đáp án
-
Đề kiểm tra Giữa kì 2 Toán 6 có đáp án (Mới nhất) - Đề 2
-
Dạng 1: tỉ số của hai đại lượng có đáp án
-
Dạng 5: Giải các bài toán thực tế có liên quan đến đoạn thẳng, độ dài đoạn thẳng và trung điểm của đoạn thẳng có đáp án
-
Dạng 4: Trung điểm của đoạn thẳng có đáp án
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận