Câu hỏi:
13/07/2024 773
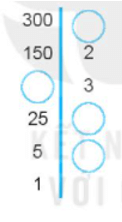
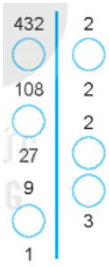
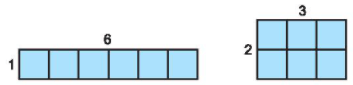
Tìm các số còn thiếu trong phân tích một số ra thừa số nguyên tố theo sơ đồ cây sau đây:
a)
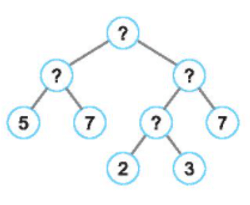
b)
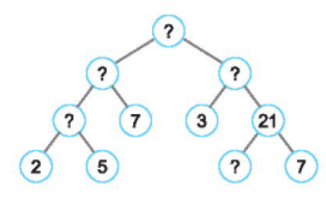
Tìm các số còn thiếu trong phân tích một số ra thừa số nguyên tố theo sơ đồ cây sau đây:
a)
b)
Câu hỏi trong đề: Giải SBT Toán lớp 6 KNTT Bài 10: Số nguyên tố có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
a)
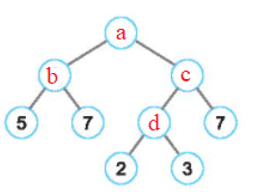
Gọi các số còn thiếu là a, b, c, d như trên hình.
+) d = 2. 3 = 6
+) c = d. 7 = 6. 7 = 42
+) b = 5. 7 = 35
+) a = b. c = 35. 42 = 1 470
Vậy ta được hình sau:
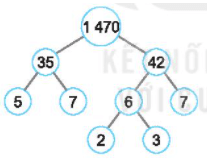
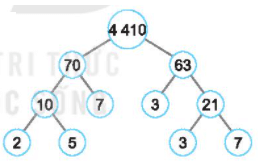
b)
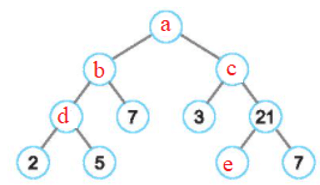
Gọi các số còn thiếu là a, b, c, d, e như trên hình.
+) 21 = e. 7 e = 21: 7 = 3
+) c = 3. 21 = 63
+) d = 2. 5 = 10
+) b = d. 7 = 10. 7 = 70
+) a = b. c = 70. 63 = 4 410
Vậy ta được hình sau:
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Tra bảng nguyên tố ta thấy 829 và 971 là số nguyên tố
Theo dấu hiệu chia hết cho 2; 3; 5 ta có 9 891 ⁝ 3; 12 344 ⁝ 2; 32 015 ⁝ 5 nên 9 891; 12 344; 32 015 là hợp số.
Lời giải
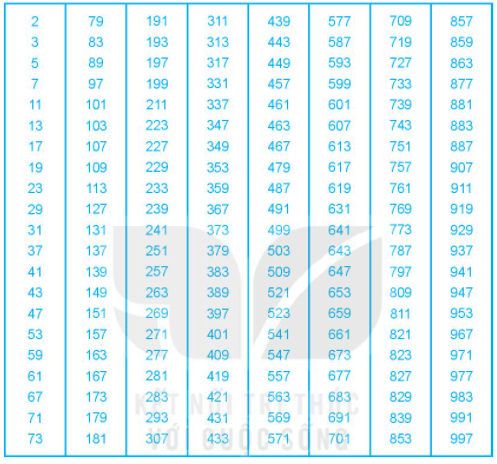
a) Từ bảng trên, ta có số 491, 499 là các số nguyên tố
Do đó để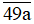 
là số nguyên tố thì a = 1 hoặc a = 9.
Vậy a = 1 hoặc a = 9.
b)
Ta có các số 233; 239 là số nguyên tố.
Do đó để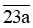 
là hợp số thì a ∈ {0; 1; 2; 3; 4; 5; 6; 7; 8; 9};
Vậy a ∈ {0; 1; 2; 3; 4; 5; 6; 7; 8; 9}.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Đề thi Cuối học kì 2 Toán 6 có đáp án (Đề 1)
-
Đề kiểm tra Giữa kì 2 Toán 6 có đáp án (Mới nhất) - Đề 1
-
31 câu Trắc nghiệm Toán 6 Kết nối tri thức Bài 1: Tập hợp có đáp án
-
Dạng 1: Thực hiện tính, viết dưới dạng lũy thừa
-
Dạng 4: Một số bài tập nâng cao về lũy thừa
-
Đề thi Cuối học kì 2 Toán 6 có đáp án (Đề 2)
-
Dạng 4: Trung điểm của đoạn thẳng có đáp án
-
Dạng 1: tỉ số của hai đại lượng có đáp án
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận