Câu hỏi:
12/07/2024 2,027
Từ điểm A nằm ngoài đường tròn (O), kẻ hai tiếp tuyến AB, AC đến đường tròn (O) (B, C là hai tiếp điểm). Vẽ cát tuyến ADE của đường tròn (O) (điểm D nằm giữa hai điểm A và E), gọi I là trung điểm của DE.
a) Chứng minh: OI DE và 5 điểm A, B, I, O, C cùng thuộc một đường tròn.
Từ điểm A nằm ngoài đường tròn (O), kẻ hai tiếp tuyến AB, AC đến đường tròn (O) (B, C là hai tiếp điểm). Vẽ cát tuyến ADE của đường tròn (O) (điểm D nằm giữa hai điểm A và E), gọi I là trung điểm của DE.
a) Chứng minh: OI DE và 5 điểm A, B, I, O, C cùng thuộc một đường tròn.Câu hỏi trong đề: Đề thi Học kì 2 Toán 9 có đáp án năm 2022-2023 !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
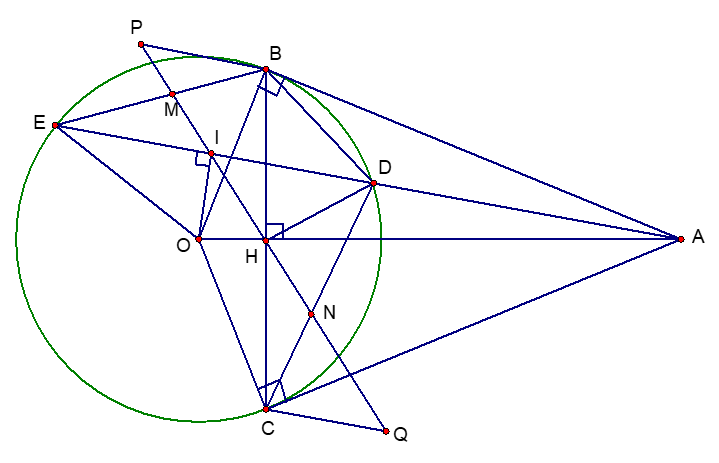
a) Chứng minh: OIDE và 5 điểm A, B, I, O, C cùng thuộc một đường tròn.
Ta có: OI là một phần đường kính, I là trung điểm của DE và DE là dây không qua tâm.
Nên OIDE
* Chứng minh 5 điểm A, B, I, O, C cùng thuộc một đường tròn
Ta có: ABO nội tiếp đường tròn đường kính OA (ABO vuông tại B)
ACO nội tiếp đường tròn đường kính OA (ACO vuông tại C)
AIO nội tiếp đường tròn đường kính OA (AIO vuông tại I)
Suy ra 5 điểm A, B, I, O, C cùng thuộc một đường tròn đường kính OA.
Hot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
b) Chứng minh: AB2 = AD.AE và AO BC tại H.
Hai ABD và AEB có:
là góc chung
(góc n/t và góc tạo bởi tia t/t và d/c cùng chắn cung BC)
Vậy ABD AEB (g-g)
* Chứng minh: AOBC tại H.
Ta có: OB = OC (bán kính (O)) và AB = AC (tính chất 2 tiếp tuyến cắt nhau)
Suy ra OA là đường trung trực của BC
Lời giải
Gọi x là số tiền lúc đầu ông A đã gửi vào ngân hàng (x > 0)
Tiền lãi một năm ông A nhận được từ ngân hàng: x.6,5%
Theo đề bài, ta có phương trình: x + 0,065x = 53250000
Suy ra x = 50.000.000
Vậy ông A đã gửi 50.000.000 đồng tiết kiệm vào ngân hàng.Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo