Cho điểm M nằm ngoài đường tròn $\left(O;R\right)$ . Từ M kẻ các tiếp tuyến MA, MB tới đường tròn tâm O (A, B là các tiếp điểm). Gọi H là giao điểm của MO với AB.

Nếu OM=2R hãy tính độ dài MA theo R và số đo các góc $\angle AMB,\angle AOB$ ?

Đồ thị hàm số $y=\left(m+1\right)x+6$  với $m\ne -1$  là đường thẳng cắt Ox tại điểm $A^{\text{'}}\left(-\frac{6}{m+1};0\right)$  và cắt Oy tại điểm  $B\left(0;6\right)$

Suy ra: $O{A}^{\text{'}}=\left|\frac{-6}{m+1}\right|=\frac{6}{\left|m+1\right|}$  và $OB=\left|6\right|=6$  

Kẻ $OH\perp A^{\text{'}}B$  tại H thì OH chính là khoảng cách từ O đến đường thẳng  $\left(d\right)$

Ta có:

$$\begin{gathered} \frac{1}{O{H}^2}=\frac{1}{O{A^{\text{'}}}^2}+\frac{1}{O{B}^2}\iff \frac{1}{{\left(3\sqrt{2}\right)}^2}=\frac{1}{{\left(\frac{6}{\left|m+1\right|}\right)}^2}=\frac{1}{6^2} \\ \iff \frac{1}{16}=\frac{1}{\frac{36}{{\left(m+1\right)}^2}}+\frac{1}{36}\iff \frac{1}{18}=\frac{{\left(m+1\right)}^2+1}{36} \\ \iff \frac{2}{36}=\frac{m^2+2m+1+1}{36}\iff 2=m^2+2m+2 \\ \iff m^2+2m=0\iff m\left(m+2\right)=0 \\ \iff \left[\begin{array}{l}m=0\\ m+2=0\end{array}\right.\iff \left[\begin{array}{l}m=0\\ m=-2\end{array}\right.\left(tmdk\right) \end{gathered}$$

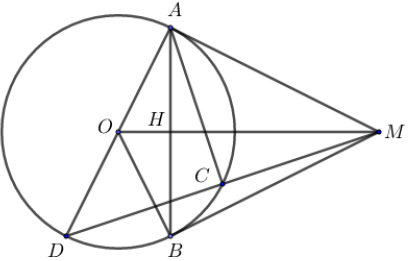
MA, MB là các tiếp tuyến của M đến đường tròn  $\left(O;R\right)$

 $\Rightarrow \angle OAM=\angle OBM=90°$

 $\Rightarrow$A, B thuộc đường tròn đường kính OM

$\Rightarrow$ M, A, O, B cùng thuộc một đường tròn (đpcm).