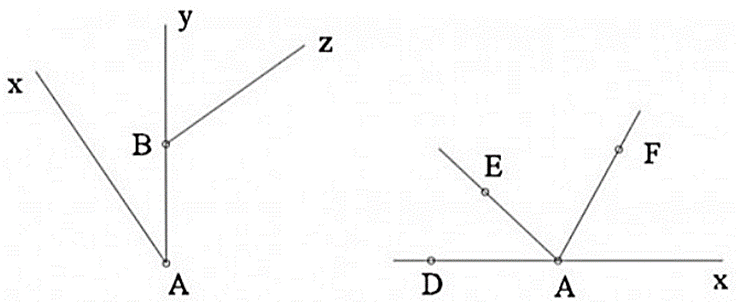
c) EF cắt CB tại I. CM tam giác AFC đồng dạng với tam giác BFD, suy ra FE là tia phân giác của góc CFD.
c) EF cắt CB tại I. CM tam giác AFC đồng dạng với tam giác BFD, suy ra FE là tia phân giác của góc CFD.
Câu hỏi trong đề: 5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án !!
Quảng cáo
Trả lời:
c) Ax // By (cùng AB), theo định lí Ta-lét ta có:
Mà CE = CA và ED = BD
=>
Lại có
Do đó ΔAFC ᔕ ΔBFD (c.g.c) (đpcm)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
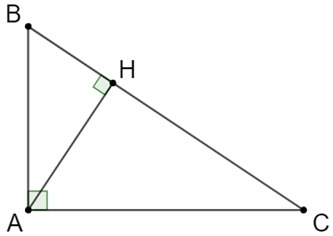
Do ∆ABC là tam giác vuông tại A nên:
Mặt khác theo định lý Pytago thì:
BC2 = AB2 + AC2
Do đó ta có đpcm.
Lời giải
Gọi 3 số hạng lần lượt là x, x + d, x + 2d (với d là công sai của cấp số cộng).
Do tổng của chúng là 27 nên ta có: x + x + d + x + 2d = 27
<=> 3x + 3d = 27
<=> x + d = 9
<=> d = 9 – x.
Tổng các bình phương của chúng là 293 nên suy ra:
x2 + (x + d)2 + (x + 2d)2 = 293
<=> x2 + (x + 9 − x)2 + (x + 18 − 2x)2 = 293
<=> x2 + 92 + (18 − x)2 = 293
<=> x2 + 81 + 324 − 36x + x2 = 293
<=> 2x2 − 36x + 112 = 0
<=> x2 − 18x + 56 = 0
<=> (x − 14)(x − 4) = 0
• TH1: Với x = 14, d = −5 thì 3 số hạng cần tìm là 14; 9; 4;
• TH2: Với x = 4, d = 5 thì 3 số hạng cần tìm là 4; 9; 14.
Vậy 3 số hạng liên tiếp cần tìm là 4; 9; 14 hoặc 14; 9; 4.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.