Câu hỏi trong đề: 5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án !!
Quảng cáo
Trả lời:
d) Ta có: CA = CE; OA = OE => OC là đường trung trực của AE
Mà AE EB => OC // EB hay OC // BK
Lại có O là trung điểm của BC
=> C là trung điểm của AK => AC = CK
EF // AK =>
Mà AC = CK => IE = IF
Gọi P = IM Ax; Q = IN By
Ta có: CP // IF =>
PA // IE =>
Mà IE = IF => CP = MP => P là trung điểm của AC.
Chứng minh tương tự ta có Q là trung điểm của BD.
IE // BD =>
và
=> ΔPCI ᔕ ΔQBI (c.g.c)
=> P, I, Q thẳng hàng Þ M, I, N thẳng hàng (đpcm)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
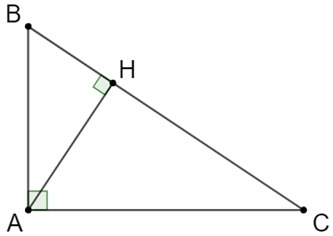
Do ∆ABC là tam giác vuông tại A nên:
Mặt khác theo định lý Pytago thì:
BC2 = AB2 + AC2
Do đó ta có đpcm.
Lời giải
Gọi 3 số hạng lần lượt là x, x + d, x + 2d (với d là công sai của cấp số cộng).
Do tổng của chúng là 27 nên ta có: x + x + d + x + 2d = 27
<=> 3x + 3d = 27
<=> x + d = 9
<=> d = 9 – x.
Tổng các bình phương của chúng là 293 nên suy ra:
x2 + (x + d)2 + (x + 2d)2 = 293
<=> x2 + (x + 9 − x)2 + (x + 18 − 2x)2 = 293
<=> x2 + 92 + (18 − x)2 = 293
<=> x2 + 81 + 324 − 36x + x2 = 293
<=> 2x2 − 36x + 112 = 0
<=> x2 − 18x + 56 = 0
<=> (x − 14)(x − 4) = 0
• TH1: Với x = 14, d = −5 thì 3 số hạng cần tìm là 14; 9; 4;
• TH2: Với x = 4, d = 5 thì 3 số hạng cần tìm là 4; 9; 14.
Vậy 3 số hạng liên tiếp cần tìm là 4; 9; 14 hoặc 14; 9; 4.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.