Cho tam giácABC Vuông cân đỉnh A .Đường tròn đường kính AD cắt BC tại D(D khác B).Điểm M bất kì trên đoạn AD ,kẻ MH, MI lần lượt vuông góc với AB và $A C (H \in A B; I \in A C)$ .

1) Chứng minh :Tứ giác $M D C I$ nội tiếp;

2) Chứng minh : $M I D = M B C;$

3) Kẻ $H K ⊥ I D (K \in I D)$ Chứng minh: $K; M; B$ thẳng hàng;

4) Khi M di động trên đoạn AD chứng minh rằng đường thẳngHK luôn đi qua một điểm có định

Câu hỏi trong đề: Tổng hợp đề thi giữa học kì 2 Toán 9 hay nhất năm 2023 có đáp án !!

Sách mới 2k7: Tổng ôn Toán, Lí, Hóa, Văn, Sử, Địa... kỳ thi tốt nghiệp THPT Quốc gia 2025, đánh giá năng lực (chỉ từ 70k).

Quảng cáo

Trả lời:

Giải bởi Vietjack

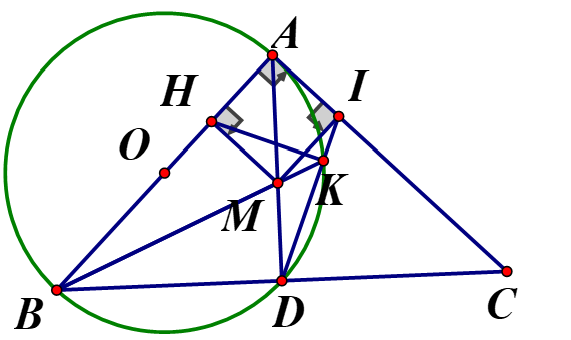
1, Vì $∠ M D C + ∠ M I C = 90 ° + 90 ° = 180 ° \Rightarrow M D I C$ là tứ giác nội tiếp

2) MDCI là tứ giác nội tiếp $\Rightarrow ∠ M I D = ∠ M C D (1)$

$Δ A B C$ vuông cân $\Rightarrow ∠ A B D = 45 ° \Rightarrow Δ A B D$ cũng vuông cân

$\Rightarrow ∠ B A D = 45 ° \Rightarrow ∠ B A D = ∠ D A C = 45 ° \Rightarrow A D$ là phân giác $∠ B A C$

$\Rightarrow Δ B A C$ cân tại A có AD phân giác nên cũng là đường trung trực $\Rightarrow M B = M C$

$\Rightarrow ∠ M B D = ∠ M C D (2)$

Từ (1) và (2) suy ra $∠ M I D = ∠ M B D = ∠ M B C (d f c m)$

3) Ta có : $H K ⊥ I D \Rightarrow ∠ H A I + ∠ I K H = 180 ° \Rightarrow A H K I$ là tứ giác nội tiếp

Mà AHMI cũng nội tiếp nên $A, H, K, M, I$ thuộc một đường tròn

$\Rightarrow A M K I$ là tứ giác nội tiếp $\Rightarrow ∠ A M K = 90 ° - ∠ H A M = 45 °$

Lại có : $∠ D I C = ∠ D M C = ∠ B M D$ (MD là trung trực của $B C)$

$\Rightarrow ∠ H M A + ∠ H M B + ∠ A M K = ∠ A M B + ∠ B M D + ∠ H M A = ∠ A M D = 180 °$

$\Rightarrow ∠ B M K = 180 ° \Rightarrow B, M, K$ thẳng hàng.

Combo - Sổ tay kiên thức trọng tâm Toán, Lí, Hóa dành cho 2k7 VietJack

Sách - Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 cho 2k7 VietJack

Sách Combo - Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) - 2025 cho 2k7 VietJack

Sách - Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 cho 2k7 VietJack

Bình luận hoặc Báo cáo
về câu hỏi!

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1:

Xem đáp án » 12/07/2024 209

Câu 2:

Xem đáp án » 02/03/2023 203

Câu 3:

Xem đáp án » 02/03/2023 193

Câu 4:

Xem đáp án » 12/07/2024 177