Câu hỏi:

12/07/2024 614

Cho hàm số bậc nhất y = (m − 1)x + m − 3 (m ≠ 1) có đồ thị là đường thẳng d.

a) Khi m = 0, hãy vẽ đồ thị hàm số trên;

Xem lời giải

Câu hỏi trong đề: 5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

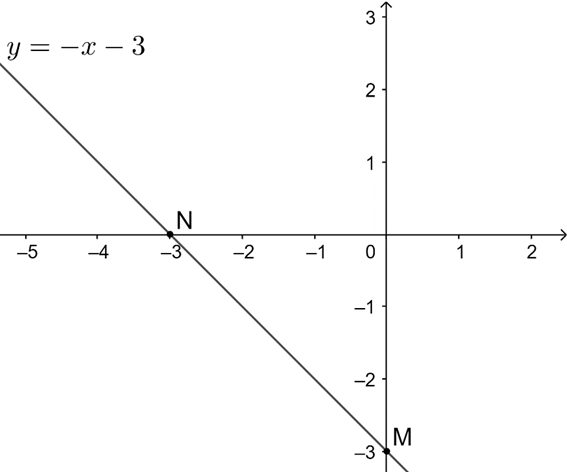
a) Với m = 0 => y = − x − 3

Ta lập bảng:

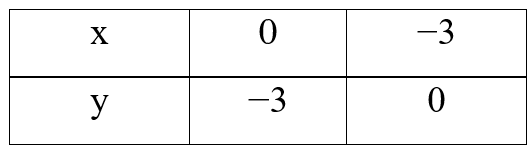
Cho hàm số bậc nhất y  (m − 1)x + m − 3 (m ≠ 1) có đồ thị là đường thẳng d. a) Khi m  0, hãy vẽ đồ thị hàm số trên; (ảnh 1)

Hàm số y = − x − 3 đi qua hai điểm M(0; −3) và N(−3; 0).

Cho hàm số bậc nhất y  (m − 1)x + m − 3 (m ≠ 1) có đồ thị là đường thẳng d. a) Khi m  0, hãy vẽ đồ thị hàm số trên; (ảnh 2)

Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Cho tam giác ABC vuông tại A, đường cao AH, AB = 6 cm, AC = 8 cm.
a) Tính BC, BH, HC, AH .

Xem đáp án

Lời giải

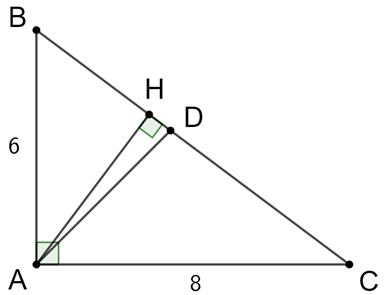
Cho tam giác ABC vuông tại A, đường cao AH, AB  6 cm, AC  8 cm. a) Tính BC, BH, HC, AH . (ảnh 1)

a) Vì ∆ABC vuông tại A nên ta có:

BC² = AB² + AC²

=> BC² = 6² + 8² = 100

=> BC = 10 cm.

Áp dụng hệ thức lượng trong tam giác vuông, ta có:

$\frac{1}{A H^{2}} = \frac{1}{A B^{2}} + \frac{1}{A C^{2}} \Leftrightarrow \frac{1}{A H^{2}} = \frac{1}{6^{2}} + \frac{1}{8^{2}} = \frac{25}{576} \Rightarrow A H = \frac{24}{5} = 4, 8 (c m)$

Áp dụng hệ thức lượng trong tam giác vuông, ta có:

AB² = BA.BC

<=> 6² = BH.10

$\Leftrightarrow B H = \frac{36}{10} = 3, 6 (c m)$

=> HC = BC − BH = 10 − 3,6 = 6,4 (cm)

Vậy BC = 10 cm, BH = 3,6 cm, HC = 6,4 cm, AH = 4,8 cm.

Câu 2

Cho phương trình: x² − mx + m − 1 = 0 (1). Tìm m để phương trình (1) có hai nghiệm phân biệt x₁ và x₂ thoả mãn: x₁² + 3x₁x₂ = 3x₂ + 3m + 16.

Xem đáp án

Lời giải

• Xét phương trình: x² − mx + m − 1 = 0 (1)

Ta có: ∆ = m² − 4(m − 1) = m² − 4m + 4 = (m − 2)²

Để phương trình có hai nghiệm phân biệt thì ∆ > 0

Hay (m − 2)² > 0 <=> m ≠ 2

Theo hệ thức Vi-ét ta có:

$\{\begin{cases} x_{1} + x_{2} = m \\ x_{1} x_{2} = m - 1 \end{cases} \Leftrightarrow \{\begin{cases} x_{1} = m - x_{2} \\ (m - x_{2}) x_{2} = m - 1 \end{cases} \Leftrightarrow \{\begin{cases} x_{1} = m - x_{2} \\ {x_{2}}^{2} - m x_{2} + m - 1 = 0 \end{cases} \Leftrightarrow \{\begin{cases} x_{1} = m - x_{2} \\ (x_{2} - 1) (x_{2} + 1) - m (x_{2} - 1) = 0 \end{cases} \Leftrightarrow \{\begin{cases} x_{1} = m - x_{2} \\ (x_{2} - 1) (x_{2} + 1 - m) = 0 \end{cases} \Leftrightarrow \{\begin{cases} x_{1} = m - x_{2} \\ [\begin{array}{l} x_{2} = 1 \\ x_{2} = m - 1 \end{array} \end{cases} \Leftrightarrow [\begin{array}{l} \{\begin{cases} x_{1} = m - 1 \\ x_{2} = 1 \end{cases} \\ \{\begin{cases} x_{1} = 1 \\ x_{2} = m - 1 \end{cases} \end{array}$

• Xét phương trình: x₁² + 3x₁x₂ = 3x₂ + 3m + 16 (2)

+) TH1: $\{\begin{cases} x_{1} = m - 1 \\ x_{2} = 1 \end{cases}$

Khi đó phương trình (2) trở thành:

(2) <=> (m − 1)² + 3(m − 1) = 3 + 3m + 16

<=> m² − 2m − 21 = 0

$\Leftrightarrow [\begin{array}{l} m = 1 + \sqrt{22} \\ m = 1 - \sqrt{22} \end{array}$

+) TH2: $\{\begin{cases} x_{1} = 1 \\ x_{2} = m - 1 \end{cases}$

Khi đó phương trình (2) trở thành:

(2) <=> 1² + 3(m − 1) = 3(m − 1) + 3m + 16

<=> 3m + 15 = 0

<=> m = −5.

Vậy $m = 1 \pm \sqrt{22}$ và m = −5 là các giá trị của m thỏa mãn.

Câu 3