Cho ∆ABC cân tại A, trung tuyến AM. Gọi I là trung điểm của AC, K là điểm đối xứng của điểm M qua điểm I.
a) Tứ giác AMCK là hình gì?
b) Tứ giác AKMB là hình gì?
c) Có trường hợp nào của ∆ABC để tứ giác AKMB là hình thoi không? Vì sao?
Cho ∆ABC cân tại A, trung tuyến AM. Gọi I là trung điểm của AC, K là điểm đối xứng của điểm M qua điểm I.
a) Tứ giác AMCK là hình gì?
b) Tứ giác AKMB là hình gì?
c) Có trường hợp nào của ∆ABC để tứ giác AKMB là hình thoi không? Vì sao?
Câu hỏi trong đề: 5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Lời giải
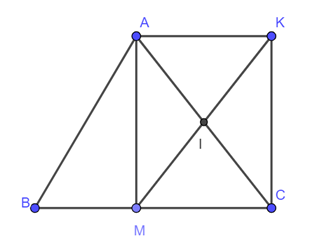
a) Áp dụng tính chất của ∆ cân cho DABC ta có: AM ⊥ MC và BM = MC
Vì I là trung điểm của AC và K đối xứng với M qua I nên tứ giác AMCK là hình bình hành.
Lại có MK = AC (= 2MI).
Do đó, tứ giác AMCK là hình chữ nhật.
b) Vì tứ giác AMCK là hình chữ nhật (theo câu a).
Do đó AK // MC và AK = MC = MB.
Vậy tứ giác AKMB là hình bình hành.
c) Nếu tứ giác AKMB là hình thoi thì BA = AK = KM = MB.
Vì DMBA cân tại B nên \[\widehat {BAM} = \widehat {AMB}\] = 90° (vô lí).
Vậy không có trường hợp nào của DABC để AKMB là hình thoi.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Lời giải
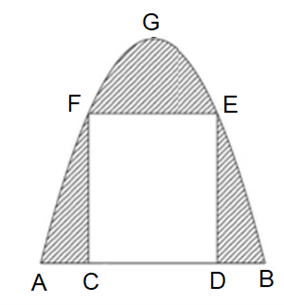
Đỉnh G có tọa độ (0; 4) nên a . 02 + b . 0 + c = 4
Do đó c = 4.
Điểm D có tọa độ (2; 3) nên a . 22 + b . 2 + 4 = 3
⇔ 4a + 2b = −14 (1)
Điểm C có tọa độ (–2; 3) nên a . (−2)2 + b . (−2) + 4 = 3
⇔ 4a – 2b = −14 (2)
Từ (1) và (2) suy ra a = – 0,25; b = 0.
Khi đó parabol có dạng y = −0,25 . x2 + 4
Điểm A và B có tung độ y = 0
⇔ −0,25 . x2 + 4 = 0
⇔ x = 4 hoặc x = – 4
Suy ra điểm B có tọa độ (4; 0) và điểm A có tọa độ (– 4; 0).
Vậy khoảng cách giữa hai điểm A và B là 8.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Lời giải
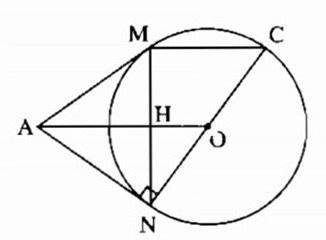
a) Ta có: AN = AM (tính chất tiếp tuyến)
Suy ra ∆AMN cân tại A
Mặt khác, OA là tia phân giác cũng là đường cao
Do đó OA ⊥ MN (đpcm).
b) Đặt H là giao điểm của MN và AO.
Ta có MH = HN (OA ⊥ MN nên H là trung điểm MN).
Mà CO = CN = R.
Suy ra OH là đường trung bình của ∆MNC.
Do đó OH // MC hay MC // OA (đpcm).
c) Ta có OM = ON = R nên ON = 3 cm.
Ta có: ON2 + AN2 = AO2 (theo định lý Py-ta-go)
Suy ra AN2 = AO2 – ON2 = 52 – 32 = 25 – 9 = 16
⇒ AN = \[\sqrt {16} \] = 4 (cm)
Ta có: AO.HN = AN.NO (hệ thức lượng trong tam giác vuông).
Suy ra 5HN = 4 . 3 = 12 ⇒ HN = \[\frac{{12}}{5}\] = 2,4 (cm).
Ta có MN = 2HN = 2 . 2,4 = 4,8 (vì H là trung điểm MN).
Vậy AM = AN = 4 cm; MN = 4,8 cm.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập