Câu hỏi:
13/07/2024 1,062
Cho hình bình hành ABCD có BC = 2AB và \[\widehat A = 60^\circ \]. Gọi E, F theo thứ tự là trung điểm của BC và AD.
a) Tứ giác ECDF là hình gì? Vì sao?
b) Tam giác DEC là tam giác gì? Vì sao?
c) Tính số đo\[\widehat {AED}\]?
Cho hình bình hành ABCD có BC = 2AB và \[\widehat A = 60^\circ \]. Gọi E, F theo thứ tự là trung điểm của BC và AD.
a) Tứ giác ECDF là hình gì? Vì sao?
b) Tam giác DEC là tam giác gì? Vì sao?
c) Tính số đo\[\widehat {AED}\]?
Câu hỏi trong đề: 5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Lời giải
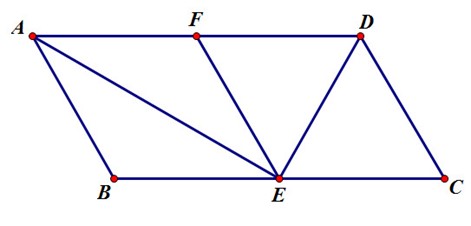
a) Ta có \[\left\{ \begin{array}{l}BC = 2AD = 2AB = 2AE = 2FD\\BC = 2BE = 2EC\end{array} \right.\]
Suy ra AB = BE = EC = CD = FD = AF
Tứ giác ECFD có \[\left\{ \begin{array}{l}FD//EC\\FD = EC\end{array} \right.\]
Do đó tứ giác ECFD là hình bình hành.
b) ∆ DEC có: \[\left\{ \begin{array}{l}DC = EC\\\widehat A = \widehat C = 60^\circ \end{array} \right.\] ⇒ ∆ DEC là ∆ đều
c) Ta có: tứ giác ABEF là hình bình hành nên AB // FE ⇒ \[\widehat {AEF} = \widehat {EAB}\] (1)
• Xét ∆AFE có AF = FE nên ∆AFE là tam giác cân.
Do đó \[\widehat {FAE} = \widehat {FEA}\] (2)
Từ (1) và (2) suy ra \[\widehat {BAE} = \widehat {EAF} = \widehat {FEA} = \frac{{60^\circ }}{2} = 30^\circ \].
• Xét ∆FED có \[\left\{ \begin{array}{l}FD = DC = DE\\\widehat {FDE} = 60^\circ \end{array} \right.\] nên ∆FED là tam giác đều.
Suy ra \[\widehat {FDE} = \widehat {DEF} = \widehat {EFD} = \frac{{180^\circ }}{3} = 60^\circ \].
Ta có \[\widehat {AED} = \widehat {AEF} + \widehat {FED} = 30^\circ + 60^\circ = 90^\circ \]
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Lời giải
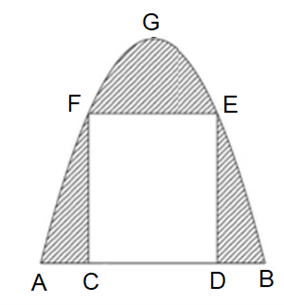
Đỉnh G có tọa độ (0; 4) nên a . 02 + b . 0 + c = 4
Do đó c = 4.
Điểm D có tọa độ (2; 3) nên a . 22 + b . 2 + 4 = 3
⇔ 4a + 2b = −14 (1)
Điểm C có tọa độ (–2; 3) nên a . (−2)2 + b . (−2) + 4 = 3
⇔ 4a – 2b = −14 (2)
Từ (1) và (2) suy ra a = – 0,25; b = 0.
Khi đó parabol có dạng y = −0,25 . x2 + 4
Điểm A và B có tung độ y = 0
⇔ −0,25 . x2 + 4 = 0
⇔ x = 4 hoặc x = – 4
Suy ra điểm B có tọa độ (4; 0) và điểm A có tọa độ (– 4; 0).
Vậy khoảng cách giữa hai điểm A và B là 8.
Lời giải
Lời giải
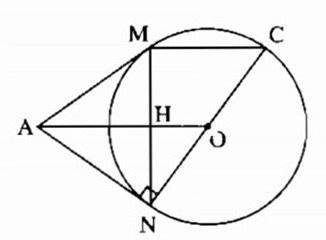
a) Ta có: AN = AM (tính chất tiếp tuyến)
Suy ra ∆AMN cân tại A
Mặt khác, OA là tia phân giác cũng là đường cao
Do đó OA ⊥ MN (đpcm).
b) Đặt H là giao điểm của MN và AO.
Ta có MH = HN (OA ⊥ MN nên H là trung điểm MN).
Mà CO = CN = R.
Suy ra OH là đường trung bình của ∆MNC.
Do đó OH // MC hay MC // OA (đpcm).
c) Ta có OM = ON = R nên ON = 3 cm.
Ta có: ON2 + AN2 = AO2 (theo định lý Py-ta-go)
Suy ra AN2 = AO2 – ON2 = 52 – 32 = 25 – 9 = 16
⇒ AN = \[\sqrt {16} \] = 4 (cm)
Ta có: AO.HN = AN.NO (hệ thức lượng trong tam giác vuông).
Suy ra 5HN = 4 . 3 = 12 ⇒ HN = \[\frac{{12}}{5}\] = 2,4 (cm).
Ta có MN = 2HN = 2 . 2,4 = 4,8 (vì H là trung điểm MN).
Vậy AM = AN = 4 cm; MN = 4,8 cm.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 1)
-
79 câu Chuyên đề Toán 12 Bài 2 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
87 câu Chuyên đề Toán 12 Bài 3 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
80 câu Trắc nghiệm Tích phân có đáp án (Phần 1)
-
56 câu Chuyên đề Toán 12 Bài 2: Lôgarit có đáp án
-
135 câu Bài tập Hình học mặt nón, mặt trụ, mặt cầu cực hay có lời giải (P1)
-
15 câu Trắc nghiệm Số phức có đáp án (Vận dụng)
-
20 câu Trắc nghiệm Phương trình đường thẳng trong không gian có đáp án (Nhận biết)